
ЁОЬтФПЁПСНИіЗДБШР§КЏЪ§yЃН![]() КЭyЃН
КЭyЃН![]() дкЕквЛЯѓЯоФкЕФЭМЯѓШчЭМЫљЪОЃЌЕуPдкyЃН
дкЕквЛЯѓЯоФкЕФЭМЯѓШчЭМЫљЪОЃЌЕуPдкyЃН![]() ЕФЭМЯѓЩЯЃЌPCЁЭxжсгкЕуCЃЌНЛyЃН
ЕФЭМЯѓЩЯЃЌPCЁЭxжсгкЕуCЃЌНЛyЃН![]() ЕФЭМЯѓгкЕуAЃЌPDЁЭyжсгкЕуDЃЌНЛyЃН
ЕФЭМЯѓгкЕуAЃЌPDЁЭyжсгкЕуDЃЌНЛyЃН![]() ЕФЭМЯѓгкЕуBЃЌЕБЕуPдкyЃН
ЕФЭМЯѓгкЕуBЃЌЕБЕуPдкyЃН![]() ЕФЭМЯѓЩЯдЫЖЏЪБЃЌвдЯТНсТлЃКЂйЁїODBгыЁїOCAЕФУцЛ§ЯрЕШЃЛЂкЫФБпаЮPAOBЕФУцЛ§ВЛЛсЗЂЩњБфЛЏЃЛЂлPAгыPBЪМжеЯрЕШЃЛЂмЕБЕуAЪЧPCЕФжаЕуЪБЃЌЕуBвЛЖЈЪЧPDЕФжаЕуЃЎЦфжавЛЖЈе§ШЗЕФЪЧ(ЁЁ ЁЁ)
ЕФЭМЯѓЩЯдЫЖЏЪБЃЌвдЯТНсТлЃКЂйЁїODBгыЁїOCAЕФУцЛ§ЯрЕШЃЛЂкЫФБпаЮPAOBЕФУцЛ§ВЛЛсЗЂЩњБфЛЏЃЛЂлPAгыPBЪМжеЯрЕШЃЛЂмЕБЕуAЪЧPCЕФжаЕуЪБЃЌЕуBвЛЖЈЪЧPDЕФжаЕуЃЎЦфжавЛЖЈе§ШЗЕФЪЧ(ЁЁ ЁЁ)
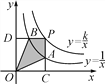
A. ЂйЂкЂл B. ЂкЂлЂм C. ЂйЂкЂм D. ЂйЂлЂм
ЁОД№АИЁПC
ЁОНтЮіЁП
ЂйгЩгкЕуAКЭЕуDОљдкЭЌвЛИіЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯ,ЫљвдSЁїODB=
ЕФЭМЯѓЩЯ,ЫљвдSЁїODB=![]() ,SЁїOCA=
,SЁїOCA=![]()
,ЙЪЁїODBгыЁїOCAЕФУцЛ§ЯрЕШ,ЙЪБОбЁЯюе§ШЗ,ЂкИљОнЗДБШР§КЏЪ§ЕФМИКЮвтвх,ЫФБпаЮPAOBЕФУцЛ§ЪМжеЕШгк|k|-1,ЙЪБОбЁЯюе§ШЗ,ЂлгЩЭМПЩжЊ,ЕБOCЃМODЪБ,PAЃОPB,ЙЪБОбЁЯюДэЮѓ,ЂмгЩгкЗДБШР§КЏЪ§ЪЧжсЖдГЦЭМаЮ,ЕБAЮЊPCЕФжаЕуЪБ,BЮЊPDЕФжаЕу,ЙЪБОбЁЯюе§ШЗ,ЙЪбЁC.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЯьгІЁАбЇРзЗцЁЂЪїаТЗчЁЂзіЮФУїжабЇЩњЁБКХейЃЌФГаЃПЊеЙСЫжОдИепЗўЮёЛюЖЏЃЌЛюЖЏЯюФПгаЁАНфЖОаћДЋЁБЁЂЁАЮФУїНЛЭЈИкЁБЁЂЁАЙиАЎРЯШЫЁБЁЂЁАвхЮёжВЪїЁБЁЂЁАЩчЧјЗўЮёЁБЕШЮхЯюЃЌЛюЖЏЦкМфЃЌЫцЛњГщШЁСЫВПЗжбЇЩњЖджОдИепЗўЮёЧщПіНјааЕїВщЃЌНсЙћЗЂЯжЃЌБЛЕїВщЕФУПУћбЇЩњЖМВЮгыСЫЛюЖЏЃЌзюЩйЕФВЮгыСЫ1ЯюЃЌзюЖрЕФВЮгыСЫ5ЯюЃЌИљОнЕїВщНсЙћЛцжЦСЫШчЭМЫљЪОВЛЭъећЕФелЯпЭГМЦЭМКЭЩШаЮЭГМЦЭМЃЎ

ЃЈ1ЃЉБЛЫцЛњГщШЁЕФбЇЩњЙВгаЖрЩйУћЃП
ЃЈ2ЃЉдкЩШаЮЭГМЦЭМжаЃЌЧѓЛюЖЏЪ§ЮЊ3ЯюЕФбЇЩњЫљЖдгІЕФЩШаЮдВаФНЧЕФЖШЪ§ЃЌВЂВЙШЋелЯпЭГМЦЭМЃЛ
ЃЈ3ЃЉИУаЃЙВгабЇЩњ2000ШЫЃЌЙРМЦЦфжаВЮгыСЫ4ЯюЛђ5ЯюЛюЖЏЕФбЇЩњЙВгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЬьУЈЩЬГЧФГЭјЕъЯњЪлФГПюРЖбРЖњЛњЃЌНјМлЮЊ100дЊ![]() дкдЊЕЉМДНЋРДСйжЎМЪЃЌПЊеЙСЫЪаГЁЕїВщЃЌЕБРЖбРЖњЛњЯњЪлЕЅМлЪЧ180дЊЪБЃЌЦНОљУПдТЕФЯњЪлСПЪЧ200МўЃЌШєЯњЪлЕЅМлУПНЕЕЭ2дЊЃЌЦНОљУПдТОЭПЩвдЖрЪлГі10МўЃЎ
дкдЊЕЉМДНЋРДСйжЎМЪЃЌПЊеЙСЫЪаГЁЕїВщЃЌЕБРЖбРЖњЛњЯњЪлЕЅМлЪЧ180дЊЪБЃЌЦНОљУПдТЕФЯњЪлСПЪЧ200МўЃЌШєЯњЪлЕЅМлУПНЕЕЭ2дЊЃЌЦНОљУПдТОЭПЩвдЖрЪлГі10МўЃЎ
![]() ЩшУПМўЩЬЦЗНЕМлxдЊЃЌИУЭјЕъЦНОљУПдТЛёЕУЕФРћШѓЮЊyдЊЃЌЧыаДГіyгыxдЊжЎМфЕФКЏЪ§ЙиЯЕЃЛ
ЩшУПМўЩЬЦЗНЕМлxдЊЃЌИУЭјЕъЦНОљУПдТЛёЕУЕФРћШѓЮЊyдЊЃЌЧыаДГіyгыxдЊжЎМфЕФКЏЪ§ЙиЯЕЃЛ
![]() ИУЭјЕъгІИУШчКЮЖЈМлВХФмЪЙЕУЦНОљУПдТЛёЕУЕФРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйдЊЃП
ИУЭјЕъгІИУШчКЮЖЈМлВХФмЪЙЕУЦНОљУПдТЛёЕУЕФРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпyЃНaЃЈxЉmЃЉ+kГЦЮЊХзЮяЯпyЃНaЃЈxЉmЃЉ2+kЕФЙиСЊжБЯпЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпyЃНx2+6xЉ1ЕФЙиСЊжБЯпЃЛ
ЃЈ2ЃЉвбжЊХзЮяЯпyЃНax2+bx+cгыЫќЕФЙиСЊжБЯпyЃН2x+3ЖМОЙ§yжсЩЯЭЌвЛЕуЃЌЧѓетЬѕХзЮяЯпЕФБэДяЪНЃЛ
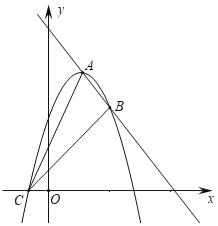
ЃЈ3ЃЉШчЭМЃЌЖЅЕудкЕквЛЯѓЯоЕФХзЮяЯпyЃНЉaЃЈxЉ1ЃЉ2+4aгыЫќЕФЙиСЊжБЯпНЛгкЕуAЃЌBЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыxжсИКАыжсНЛгкЕуCЃЌСЌНсACЁЂBCЃЎЕБЁїABCЮЊжБНЧШ§НЧаЮЪБЃЌЧѓaЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
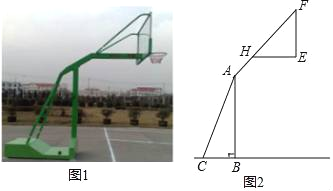
ЁОЬтФПЁПШчЭМ1ЃЌ2ЗжБ№ЪЧФГПюРКЧђМмЕФЪЕЮяЭМгыЪОвтЭМЃЌвбжЊABЁЭBCгкЕуBЃЌЕззљBCЕФГЄЮЊ1УзЃЌЕззљBCгыжЇМмACЫљГЩЕФНЧЁЯACBЃН60ЁуЃЌЕуHдкжЇМмAFЩЯЃЌРКАхЕзВПжЇМмEHЁЮBCЃЌEFЁЭEHгкЕуEЃЌвбжЊAHГЄ![]() УзЃЌHFГЄ
УзЃЌHFГЄ![]() УзЃЌHEГЄ1УзЃЎ
УзЃЌHEГЄ1УзЃЎ
(1)ЧѓРКАхЕзВПжЇМмHEгыжЇМмAFЫљГЩЕФНЧЁЯFHEЕФЖШЪ§ЃЎ
(2)ЧѓРКАхЕзВПЕуEЕНЕиУцЕФОрРыЃЎ(НсЙћБЃСєИљКХ)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
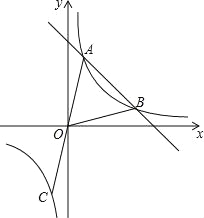
ЁОЬтФПЁПШчЭМЃЌжБЯпy=Љx+bгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓЯрНЛгкAЃЈ1ЃЌ4ЃЉЃЌBСНЕуЃЌбгГЄAOНЛЗДБШР§КЏЪ§ЭМЯѓгкЕуCЃЌСЌНгOBЃЎ
ЕФЭМЯѓЯрНЛгкAЃЈ1ЃЌ4ЃЉЃЌBСНЕуЃЌбгГЄAOНЛЗДБШР§КЏЪ§ЭМЯѓгкЕуCЃЌСЌНгOBЃЎ
ЃЈ1ЃЉЧѓkКЭbЕФжЕЃЛ
ЃЈ2ЃЉжБНгаДГівЛДЮКЏЪ§жЕаЁгкЗДБШР§КЏЪ§жЕЕФздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉдкyжсЩЯЪЧЗёДцдквЛЕуPЃЌЪЙ![]() ЃПШєДцдкЧыЧѓГіЕуPзјБъЃЌШєВЛДцдкЧыЫЕУїРэгЩЃЎ
ЃПШєДцдкЧыЧѓГіЕуPзјБъЃЌШєВЛДцдкЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊABЮЊЁбOЕФжБОЖЃЌЯвCDЁЭABЃЌДЙзуЮЊH.
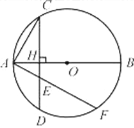
(1) ЧѓжЄЃКAH![]() AB=AC2ЃЛ
AB=AC2ЃЛ
(2) ШєЙ§AЕФжБЯпгыЯвCD(ВЛКЌЖЫЕу)ЯрНЛгкЕуEЃЌгыЁбOЯрНЛгкЕуFЃЌЧѓжЄЃКAE![]() AF=AC2ЃЛ
AF=AC2ЃЛ
(3) ШєЙ§AЕФжБЯпгыжБЯпCDЯрНЛгкЕуPЃЌгыЁбOЯрНЛгкЕуQЃЌХаЖЯAP![]() AQ=AC2ЪЧЗёГЩСЂ(ВЛБижЄУї).
AQ=AC2ЪЧЗёГЩСЂ(ВЛБижЄУї).
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌRtЁїABOЕФЖЅЕуAЪЧЗДБШР§КЏЪ§y=![]() гывЛДЮКЏЪ§y=ЉxЉЃЈk+1ЃЉЕФЭМЯѓдкЕкЖўЯѓЯоЕФНЛЕуЃЌABЁЭxжсгкBЃЌЧвSЁїABO=
гывЛДЮКЏЪ§y=ЉxЉЃЈk+1ЃЉЕФЭМЯѓдкЕкЖўЯѓЯоЕФНЛЕуЃЌABЁЭxжсгкBЃЌЧвSЁїABO=![]() ЃЎ
ЃЎ
ЃЈ1ЃЉжБНгаДГіетСНИіКЏЪ§ЕФЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓЁїAOCЕФУцЛ§ЃЛ
ЃЈ3ЃЉИљОнЭМЯѓжБНгаДГіЃКЕБxЮЊКЮжЕЪБЃЌЗДБШР§КЏЪ§ЕФжЕаЁгквЛДЮКЏЪ§ЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
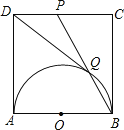
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDБпГЄЮЊ1ЃЌвдABЮЊжБОЖзїАыдВЃЌЕуPЪЧCDжаЕуЃЌBPгыАыдВНЛгкЕуQЃЌСЌНг![]() ИјГіШчЯТНсТлЃК
ИјГіШчЯТНсТлЃК![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() Цфжае§ШЗЕФНсТлЪЧ______
Цфжае§ШЗЕФНсТлЪЧ______![]() ЬюаДађКХ
ЬюаДађКХ![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com