
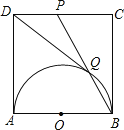
【题目】如图,正方形ABCD边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连接![]() 给出如下结论:
给出如下结论:![]() ;
;![]() ;
;![]() ;
;![]() 其中正确的结论是______
其中正确的结论是______![]() 填写序号
填写序号![]()
【答案】![]()
【解析】
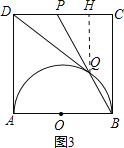
①连接OQ,OD,如图1.易证四边形DOBP是平行四边形,从而可得DO∥BP.结合OQ=OB,可证到∠AOD=∠QOD,从而证到△AOD≌△QOD,则有DQ=DA=1;
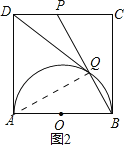
②连接AQ,如图2,根据勾股定理可求出BP.易证Rt△AQB∽Rt△BCP,运用相似三角形的性质可求出BQ,从而求出PQ的值,就可得到![]() 的值;
的值;
③过点Q作QH⊥DC于H,如图3.易证△PHQ∽△PCB,运用相似三角形的性质可求出QH,从而可求出S△DPQ的值;
④根据图1和①中的结论可作判断.
①连接OQ,OD,如图1.
易证四边形DOBP是平行四边形,从而可得DO∥BP,
∴∠AOD=∠OBP,∠DOQ=∠OQB,
∵OB=OQ,
∴∠OBP=∠OQB,
∴∠AOD=∠QOD,从而证到△AOD≌△QOD,
则有DQ=DA=1;
故①正确;
②连接AQ,如图2.
∵P是CD的中点,
∴CP=![]() CD=
CD=![]() ,BP
,BP![]() .
.![]()
易证Rt△AQB∽Rt△BCP,
∴![]() ,即
,即![]() ,
,
∴BQ=![]() ,
,
则PQ=BP﹣BQ=![]() ﹣
﹣![]() =
=![]() ,
,
∴![]() =
=![]() ;
;
故②正确;
③过点Q作QH⊥DC于H,如图3.
易证△PHQ∽△PCB,
∴![]() ,即
,即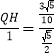
∴QH=![]() ,
,
∴S△DPQ=![]() DPQH=
DPQH=![]() .
.
故③错误;
④如图1,由①知:△AOD≌△QOD,
∴∠ADQ=2∠ODQ,
∵OD∥PB,
∴∠ODQ=∠DQP,
∴∠ADQ=2∠DQP,
故④正确,
综上所述:正确结论是①②④.
故答案为:①②④.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
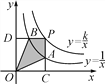
【题目】两个反比例函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=![]() 的图象上,PC⊥x轴于点C,交y=
的图象上,PC⊥x轴于点C,交y=![]() 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y=![]() 的图象于点B,当点P在y=
的图象于点B,当点P在y=![]() 的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②四边形PAOB的面积不会发生变化;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②四边形PAOB的面积不会发生变化;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在创客教育理念的指引下,国内很多学校都纷纷建立创客实践室及创客空间,致力于从小培养孩子的创新精神和创造能力,郑州市某校开设了“3D”打印、数学编程、智能机器人、陶艺制作”四门创客课程,为了解学生对这四门创客课程的喜爱情况,数学兴趣小组对全校学生进行了随机问卷调查(问卷调查表如表所示),将调查结果整理后绘制成图1、图2两幅均不完整的统计图表.

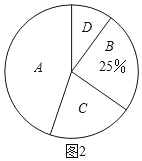
最受欢理的创客课程词查问卷
你好!这是一份关于你喜欢的创客深程问卷调查表,请你在表格中选择一个(只能选择一个)你最喜欢的课程选项在其后空格内打“√“,非常感谢你的合作.

请根据图表中提供的值息回答下列问题:
(1)统计表中的a= ,b= ;
(2)“D”对应扇形的圆心角为 ;
(3)根据调查结果,请你估计该校2000名学生中最喜欢“数学编程”创客课程的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
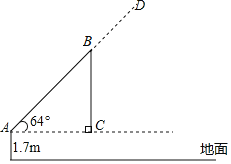
【题目】如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为![]() ,吊臂底部A距地面
,吊臂底部A距地面![]() 参考数据
参考数据![]() ,
,![]() ,
,![]() .
.
![]() 当吊臂底部A与货物的水平距离AC为5m时,吊臂AB的长为______
当吊臂底部A与货物的水平距离AC为5m时,吊臂AB的长为______![]() 计算结果精确到
计算结果精确到![]() ;
;
![]() 如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?
如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?![]() 吊钩的长度与货物的高度忽略不计
吊钩的长度与货物的高度忽略不计![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
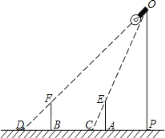
【题目】如图,高高的路灯挂在学校操场旁边上方,高傲而明亮.王刚同学拿起一根![]() 长的竹竿去测量路灯的高度,他走到路灯旁的一个地方,点
长的竹竿去测量路灯的高度,他走到路灯旁的一个地方,点![]() 竖起竹竿(
竖起竹竿(![]() 表示),这时他量了一下竹竿的影长
表示),这时他量了一下竹竿的影长![]() 正好是
正好是![]() ,他沿着影子的方向走,向远处走出两个竹竿的长度(即
,他沿着影子的方向走,向远处走出两个竹竿的长度(即![]() )到点
)到点![]() ,他又竖起竹竿(
,他又竖起竹竿(![]() 表示),这时竹竿的影长
表示),这时竹竿的影长![]() 正好是一根竹竿的长度(即
正好是一根竹竿的长度(即![]() ),此时,王刚同学抬头若有所思地说道:“噢,原来路灯有
),此时,王刚同学抬头若有所思地说道:“噢,原来路灯有![]() 高呀”.你觉得王刚同学的判断对吗?若对,请给出解答,若不对,请说明理由.
高呀”.你觉得王刚同学的判断对吗?若对,请给出解答,若不对,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线W:y=x-4x+2的顶点为A,与x轴交于点B、C.
(1)求∠ABC的正切值;
(2)若点P是抛物线W上的一点,过P作直线PQ垂直x轴,将抛物线W关于直线PQ对称,得到抛物线Wˊ,设抛物线Wˊ的顶点Aˊ,问:是否存在这样的点P,使得△APAˊ为直角三角形?若存在,求出对称所得的抛物线Wˊ的表达式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com