
 如图,点A是双曲线y=$\frac{4}{x}$(x<0)上一点,AO的延长线交双曲线y=$\frac{{k}^{2}}{x}$(x>0,k>0)于点B,BC⊥x轴,若S△ABC=7.5,则k的值为3.
如图,点A是双曲线y=$\frac{4}{x}$(x<0)上一点,AO的延长线交双曲线y=$\frac{{k}^{2}}{x}$(x>0,k>0)于点B,BC⊥x轴,若S△ABC=7.5,则k的值为3. 分析 过点A作AD⊥y轴于点D,则△AOD∽△OBC,由相似三角形的性质可得出$\frac{AD}{OC}$=$\frac{OD}{BC}$=$\sqrt{\frac{{S}_{△AOD}}{{S}_{△OBC}}}$,再根据反比例函数系数k的几何意义即可得出SAOD=$\frac{1}{2}$×4=2、SOBC=$\frac{1}{2}$k2,结合三角形的面积公式以及S△ABC=7.5即可得出关于|k|的一元二次方程,解之即可得出|k|的值,结合k>0即可得出结论.
解答 解:过点A作AD⊥y轴于点D,如图所示.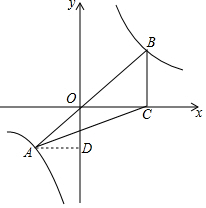
∵AD⊥y轴,BC⊥x轴,
∴AD∥OC,∠ADO=∠OCB=90°,
∴∠OAD=∠BOC,
∴△AOD∽△OBC,
∴$\frac{AD}{OC}$=$\frac{OD}{BC}$=$\sqrt{\frac{{S}_{△AOD}}{{S}_{△OBC}}}$.
∵SAOD=$\frac{1}{2}$×4=2,SOBC=$\frac{1}{2}$k2,
∴$\frac{AD}{OC}$=$\sqrt{\frac{{S}_{△AOD}}{{S}_{△OBC}}}$=$\frac{2}{|k|}$,
∴SAOC=$\frac{1}{2}$OC•OD=$\frac{1}{2}$$\frac{|k|}{2}$AD•OD=|k|.
∵S△ABC=SOBC+SOBC=$\frac{1}{2}$k2+|k|=7.5,
解得:|k|=3或|k|=-5(舍去),
∵k>0,
∴k=3.
故答案为:3.
点评 本题考查了反比例函数系数k的几何意义、相似三角形的判定与性质以及解一元二次方程,根据三角形的面积公式找出关于|k|的一元二次方程是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
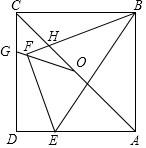 在正方形ABCD中,AB=6,点E在边AD上,DE=$\frac{1}{3}$AD.连接BE,将△ABE沿BE翻折,点A落在点F处,BF与AC交于点H,点O是AC的中点,连接OF并延长交CD于点G,则四边形GFHC的面积是$\frac{5184}{2431}$.
在正方形ABCD中,AB=6,点E在边AD上,DE=$\frac{1}{3}$AD.连接BE,将△ABE沿BE翻折,点A落在点F处,BF与AC交于点H,点O是AC的中点,连接OF并延长交CD于点G,则四边形GFHC的面积是$\frac{5184}{2431}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (79+0.8)2 | B. | (70+9.8)2 | C. | (80-0.2)2 | D. | (100-20.2)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
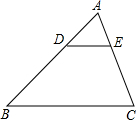 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,则下列结论中正确的是( )| A. | $\frac{AE}{AC}=\frac{1}{2}$ | B. | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ADE的面积}{△ABC的面积}=\frac{1}{3}$ | D. | $\frac{△ADE的周长}{△ABC的周长}=\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
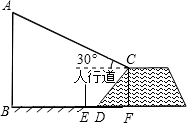 如图,欲拆除一座垂直于地面的烟囱AB,距烟囱AB水平距离14米的D处有坡度为2:1,坝高(即CF)4米的背水坡大坝,在坝顶点C处测得烟囱顶端的仰角为30°,D,E之间是宽为2m的行人道,为确保行人安全,在拆除烟囱AB时,是否需要将此人行道封闭.(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)(参考数值:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
如图,欲拆除一座垂直于地面的烟囱AB,距烟囱AB水平距离14米的D处有坡度为2:1,坝高(即CF)4米的背水坡大坝,在坝顶点C处测得烟囱顶端的仰角为30°,D,E之间是宽为2m的行人道,为确保行人安全,在拆除烟囱AB时,是否需要将此人行道封闭.(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)(参考数值:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
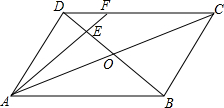 如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF:FC=( )
如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF:FC=( )| A. | 1:4 | B. | 1:3 | C. | 1:2 | D. | 1:1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com