
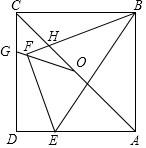
 在正方形ABCD中,AB=6,点E在边AD上,DE=$\frac{1}{3}$AD.连接BE,将△ABE沿BE翻折,点A落在点F处,BF与AC交于点H,点O是AC的中点,连接OF并延长交CD于点G,则四边形GFHC的面积是$\frac{5184}{2431}$.
在正方形ABCD中,AB=6,点E在边AD上,DE=$\frac{1}{3}$AD.连接BE,将△ABE沿BE翻折,点A落在点F处,BF与AC交于点H,点O是AC的中点,连接OF并延长交CD于点G,则四边形GFHC的面积是$\frac{5184}{2431}$. 分析 建立如图坐标系,作FN⊥AD于N,延长BF交CD于M,连接AF.首先求出点F的坐标,再求出直线BM、OG、AC的解析式,利用方程组求出点H的坐标,根据S四边形GFHC=S△CHM-S△GFM计算即可.
解答 解:建立如图坐标系,作FN⊥AD于N,延长BF交CD于M,连接AF.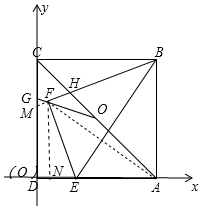
∵四边形ABCD是正方形,
∴AB=CD=BC=AD=6,
∵DE=$\frac{1}{3}$DA=2,∴AE=4,
在Rt△ABE中,BE=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$,
∵四边形ABFE的面积=$\frac{1}{2}$•AF•BE=2•$\frac{1}{2}$•AE•AB,
∴AF=$\frac{24\sqrt{13}}{13}$,
由△AFN∽△BEA,可得FN=$\frac{48}{13}$,AN=$\frac{72}{13}$,
∴DN=$\frac{6}{13}$,
∴F($\frac{6}{13}$,$\frac{48}{13}$),D(3,3),A(6,0),B(6,6),
∴直线AC的解析式y=-x+6,
直线OG的解析式y=-$\frac{3}{11}$x+$\frac{42}{11}$,可得DG=$\frac{42}{11}$,
直线BM的解析式y=$\frac{5}{12}$x+$\frac{7}{2}$,可得DM=$\frac{7}{2}$,GM=DG-DM=$\frac{7}{22}$,
由$\left\{\begin{array}{l}{y=-x+6}\\{y=\frac{5}{12}x+\frac{7}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{30}{17}}\\{y=\frac{72}{17}}\end{array}\right.$,可得H($\frac{30}{17}$,$\frac{72}{17}$),
∴S四边形GFHC=S△CHM-S△GFM=$\frac{1}{2}$•(6-$\frac{7}{2}$)×$\frac{30}{17}$-$\frac{1}{2}$×$\frac{7}{22}$×$\frac{6}{13}$=$\frac{5184}{2431}$.
点评 本题考查翻折变换、正方形的性质、勾股定理、平面坐标系、一次函数的应用等知识,解题的关键是建立平面直角坐标系,学会利用一次函数确定两条直线的交点坐标,属于中考填空题中的压轴题.


 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
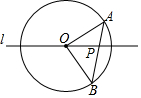 如图,已知点A、B为⊙O上的两点,且∠A=40°,直线l经过圆心O,与AB相交于点P,若直线l绕点O旋转,当△OBP为等腰三角形时,∠AOP=60°.
如图,已知点A、B为⊙O上的两点,且∠A=40°,直线l经过圆心O,与AB相交于点P,若直线l绕点O旋转,当△OBP为等腰三角形时,∠AOP=60°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点A是双曲线y=$\frac{4}{x}$(x<0)上一点,AO的延长线交双曲线y=$\frac{{k}^{2}}{x}$(x>0,k>0)于点B,BC⊥x轴,若S△ABC=7.5,则k的值为3.
如图,点A是双曲线y=$\frac{4}{x}$(x<0)上一点,AO的延长线交双曲线y=$\frac{{k}^{2}}{x}$(x>0,k>0)于点B,BC⊥x轴,若S△ABC=7.5,则k的值为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
| 人数 | 1 | 1 | 3 | 5 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
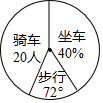 如图是七年级(21)班学生上学的不同方式的扇形统计图,若步行人数所占的圆心角的度数为72°,坐车的人数占40%,骑车人数为20人,则该班人数为50人.
如图是七年级(21)班学生上学的不同方式的扇形统计图,若步行人数所占的圆心角的度数为72°,坐车的人数占40%,骑车人数为20人,则该班人数为50人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com