
分析 计算出S1,S2,S3,以此类推得到Sn,代入原式利用平方根定义化简,再利用拆项法变形,计算即可得到结果.
解答 解:∵S1=1+$\frac{1}{{1}^{2}}$+$\frac{1}{{2}^{2}}$=$\frac{9}{4}$=($\frac{3}{2}$)2,
S2=1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$=$\frac{5}{4}$+$\frac{1}{9}$=$\frac{49}{36}$=($\frac{7}{6}$)2,
S3=1+$\frac{1}{{3}^{2}}$+$\frac{1}{{4}^{2}}$=1+$\frac{1}{9}$+$\frac{1}{16}$=$\frac{169}{144}$=($\frac{13}{12}$)2,
…,
Sn=1+$\frac{1}{{n}^{2}}$+$\frac{1}{(n+1)^{2}}$=($\frac{{n}^{2}+n+1}{n(n+1)}$)2,
∴原式=$\frac{3}{2}$+$\frac{7}{6}$+$\frac{13}{12}$+…+$\frac{{n}^{2}+n+1}{n(n+1)}$
=1+$\frac{1}{2}$+1+$\frac{1}{6}$+1+$\frac{1}{12}$+…+1+$\frac{1}{n(n+1)}$
=n+($\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$)
=n+(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)
=n+1-$\frac{1}{n+1}$
=$\frac{(n+1)^{2}-1}{n+1}$
=$\frac{{n}^{2}+2n}{n+1}$.
点评 此题考查了实数的运算,拆项法的运用,以及规律型:数字的变化类,弄清题中的规律是解本题的关键.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图:在x轴的上方,直角∠BOA绕原点O顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{1}{x}$、y=$\frac{2}{x}$的图象交于B、A两点,则tanA=$\frac{\sqrt{2}}{2}$.
如图:在x轴的上方,直角∠BOA绕原点O顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{1}{x}$、y=$\frac{2}{x}$的图象交于B、A两点,则tanA=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
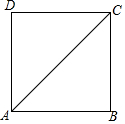 如图,正方形ABCD的对角线AC长为2$\sqrt{2}$,若直线满足:①点C到直线l的距离为1;②B、D两点到直线l的距离相等,那么符合题意的直线l有4条.
如图,正方形ABCD的对角线AC长为2$\sqrt{2}$,若直线满足:①点C到直线l的距离为1;②B、D两点到直线l的距离相等,那么符合题意的直线l有4条.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
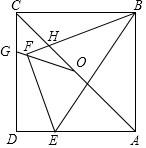 在正方形ABCD中,AB=6,点E在边AD上,DE=$\frac{1}{3}$AD.连接BE,将△ABE沿BE翻折,点A落在点F处,BF与AC交于点H,点O是AC的中点,连接OF并延长交CD于点G,则四边形GFHC的面积是$\frac{5184}{2431}$.
在正方形ABCD中,AB=6,点E在边AD上,DE=$\frac{1}{3}$AD.连接BE,将△ABE沿BE翻折,点A落在点F处,BF与AC交于点H,点O是AC的中点,连接OF并延长交CD于点G,则四边形GFHC的面积是$\frac{5184}{2431}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com