
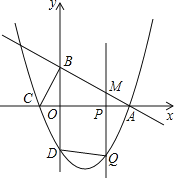
【题目】如图,在平面直角坐标系中,直线![]() 分别交x轴,y轴于点A,B抛物线
分别交x轴,y轴于点A,B抛物线![]() 经过点A,且交x轴于另外一点C,交y轴于点D.
经过点A,且交x轴于另外一点C,交y轴于点D.
(1)求抛物线的表达式;
(2)求证:AB⊥BC;
(3)点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m,当以B,D,Q,M为顶点的四边形是平行四边形时,求m的值.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)见解析;(3)m的值是2或1+
x﹣2;(2)见解析;(3)m的值是2或1+![]() 或1﹣
或1﹣![]() .
.
【解析】
(1)令y=﹣![]() x+2=0,解得:x=4,即可求解,然后把点A的坐标代入抛物线解析式,借助于方程求得a的值即可;
x+2=0,解得:x=4,即可求解,然后把点A的坐标代入抛物线解析式,借助于方程求得a的值即可;
(2)把由函数图象上点的坐标特征求得点B、C的坐标,然后利用两点间的距离公式和勾股定理的逆定理证得结论;
(3)以B、D、Q,M为顶点的四边形是平行四边形时,利用|MQ|=BD即可求解.
(1)令y=﹣![]() x+2=0,解得:x=4,y=0,则x=2,
x+2=0,解得:x=4,y=0,则x=2,
即:点A坐标为:(4,0).
代入![]() 中,得16a﹣8=0,得a=
中,得16a﹣8=0,得a=![]() .
.
∴该抛物线解析式为:y=![]() x2﹣
x2﹣![]() x﹣2.
x﹣2.
(2)由(1)知,抛物线解析式为:y=![]() x2﹣
x2﹣![]() x﹣2.
x﹣2.
∴当y=0时,x1=﹣1,x2=4,的C(﹣1,0).
故OC=1.
于是AB2=20,BC2=5,AC2=25.
从而AB2+BC2=AC2.
∴AB⊥BC;
(3)由(1)知,抛物线解析式为: ![]() .
.
当x=0时,y=2,得D(0,﹣2),
∴BD=4.
当MQ=(﹣![]() m+2)﹣
m+2)﹣![]() =
=![]() ﹣m﹣4=4时,得m=2或m=0(舍去).
﹣m﹣4=4时,得m=2或m=0(舍去).
当MQ=(![]() m2﹣
m2﹣![]() m﹣2)﹣(﹣
m﹣2)﹣(﹣![]() m+2)=
m+2)=![]() ﹣m﹣4=4时,得m=1+
﹣m﹣4=4时,得m=1+![]() 或m=1﹣
或m=1﹣![]() .
.
综上所述,m的值是2或1+![]() 或1﹣
或1﹣![]() .
.


 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
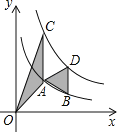
【题目】如图,点A,B在反比例函数y=![]() (x>0)的图象上,点C,D在反比例函数y=
(x>0)的图象上,点C,D在反比例函数y=![]() (k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为_____.
,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
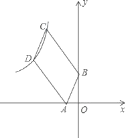
【题目】如图,已知四边形ABCD是平行四边形,BC=3AB,A,B两点的坐标分别是(﹣1,0),(0,2),C,D两点在反比例函数![]() (x<0)的图象上,则k的值等于_____.
(x<0)的图象上,则k的值等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有除颜色外其余均相同的5个小球,其中红球3个(记为A1,A2,A3),黑球2个(记为B1,B2).
(1)若先从袋中取出m(m>0)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:①若A为必然事件,则m的值为 ②若A为随机事件,则m的取值为
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,用树状图或列表法求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
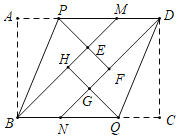
【题目】如图,在矩形纸片ABCD中,BM,DN分别平分∠ABC,∠CDA,沿BP折叠,点A恰好落在BM上的点E处,延长PE交DN于点F沿DQ折叠,点C恰好落在DN上的点G处,延长QG交BM于点H,若四边形EFGH恰好是正方形,且边长为1,则矩形ABCD的面积为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
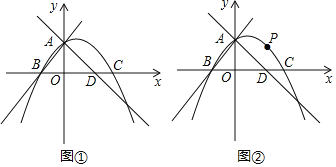
【题目】如图①,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,将直线
,将直线![]() 绕点
绕点![]() 逆时针旋转90°,所得直线与
逆时针旋转90°,所得直线与![]() 轴交于点
轴交于点![]() .
.
(1)求直线![]() 的函数解析式;
的函数解析式;
(2)如图②,若点![]() 是直线
是直线![]() 上方抛物线上的一个动点
上方抛物线上的一个动点
①当点![]() 到直线
到直线![]() 的距离最大时,求点
的距离最大时,求点![]() 的坐标和最大距离;
的坐标和最大距离;
②当点![]() 到直线
到直线![]() 的距离为
的距离为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
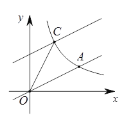
【题目】如图,直线y =![]() x与反比例函数y =
x与反比例函数y =![]() (x>0)的图象交于点A,已知点A的横坐标为4.
(x>0)的图象交于点A,已知点A的横坐标为4.
(1)求反比例函数的解析式;
(2)将直线y =![]() x向上平移3个单位后的直线l与y =
x向上平移3个单位后的直线l与y =![]() (x>0)的图象交于点C;
(x>0)的图象交于点C;
①求点C的坐标;
②记y =![]() (x>0)的图象在点A,C之间的部分与线段OA,OC围成的区域(不含边界)为W,则区域W内的整点(横,纵坐标都是整数的点)的个数为 .
(x>0)的图象在点A,C之间的部分与线段OA,OC围成的区域(不含边界)为W,则区域W内的整点(横,纵坐标都是整数的点)的个数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小刚和小红打算各自随机选择本周日的上午或下午去兴化李中水上森林游玩.
(1)小明和小刚都在本周日上午去游玩的概率为 ;
(2)求他们三人在同一个半天去游玩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成下面两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
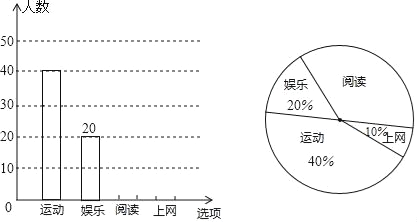
(1)在这次调查中,一共调查了 名学生;
(2)补全条形统计图;
(3)若该校共有1500名学生,估计爱好运动的学生有 人;
(4)在全校同学中随机选取一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com