
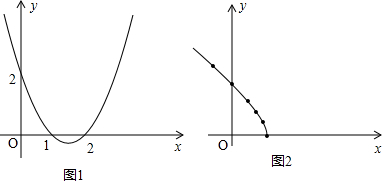
分析 (1)根据二次根式的性质,列出不等式,解之即可;
(2)由于x≤1或x≥2,所以函数图象应该是两条分支,根据对称性,补全另一分支即可;
(3)将方程的根转化为两函数图象交点的横坐标,作出函数图象,一目了然.
解答 解:(1)∵(x-1)(x-2)≥0,
∴x≤1或x≥2;
(2)根据自变量x的取值范围可知,当x≥2时也有对应的函数图象,
补全后的函数图象如下图所示: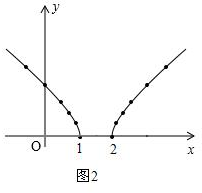
(3)方程$\sqrt{(x-1)(x-2)}$-$\frac{1}{4}$x-b=0等价于方程$\sqrt{(x-1)(x-2)}$=$\frac{1}{4}$x+b,
方程的两根x1、x2相当于函数y=$\sqrt{(x-1)(x-2)}$与函数y=$\frac{1}{4}$x+b图象的两个交点的横坐标,
方程x2-3x+2=$\frac{1}{4}$x+b的两根为x3、x4,相当于函数y=x2-3x+2=(x-1)(x-2)与函数y=$\frac{1}{4}$x+b图象的两个交点的横坐标,
又∵1<b<$\sqrt{2}$,
所以,在同一平面直角从标系中,画出函数图象,如图所示: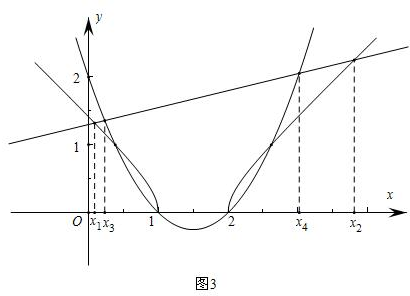
故x1<x3<x4<x2.
点评 本题主要考查了函数自变量的取值范围、函数图象的画法、函数图象的交点问题,题目新颖,但难度不大.第(3)问体现了化归与转化的数学思想,将方程与函数巧妙地结合在一起,方程的根转化为函数图象交点的横坐标,利用数形结合,将看似抽像的问题变得形像化了,从而使问题解决起来变得容易.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,B(6,0),E(0,6),直线y=3x+3与x轴、y轴交于A、C两点,∠CPE=∠CAB
如图,B(6,0),E(0,6),直线y=3x+3与x轴、y轴交于A、C两点,∠CPE=∠CAB查看答案和解析>>
科目:初中数学 来源: 题型:解答题
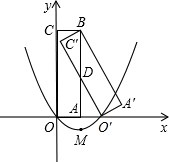 如图,矩形A′BC′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3).
如图,矩形A′BC′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com