
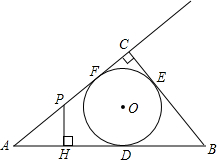
 如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.
如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.分析 (1)由勾股定理求AC的长度;设⊙O的半径为r,则r=$\frac{1}{2}$(AC+BC-AB);根据圆的切线定理、正方形的判定定理知四边形CEOF是正方形;然后由正方形的性质证得CF=OF=1,则由图中线段间的和差关系即可求得AD的长度;
(2)当点P在线段AC上时,通过相似三角形△AHP∽△ACB的对应边成比例知,$\frac{PH}{BC}$=$\frac{AP}{AB}$=$\frac{AC-PC}{AB}$,将“PH=x,PC=y”代入求出即可求得y关于x的函数关系式;(3)分两种情况,当P在线段AC上时,根据圆的切线定理证得四边形OMH′D、四边形CFOE为正方形;然后利用正方形的性质、圆的切线定理推知P′H′=P′M+MH′=P′F+FC=P′C,即x=y;最后将其代入(2)中的函数关系式即可求得y值,即PC的长;当P在线段AC的延长线上时,同理,利用相似三角形的性质求得y关于x的函数关系式,同理可求得y值,即PC的长.
解答 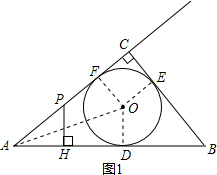 解:(1)AC=4,AD=3,⊙O的半径长为1.
解:(1)AC=4,AD=3,⊙O的半径长为1.
(如图1,连接AO、DO.设⊙O的半径为r.
在Rt△ABC中,由勾股定理得AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4,
则⊙O的半径r=$\frac{1}{2}$(AC+BC-AB)=$\frac{1}{2}$(4+3-5)=1;
∵CE、CF是⊙O的切线,∠ACB=90°,
∴∠CFO=∠FCE=∠CEO=90°,CF=CE,
∴四边形CEOF是正方形,
∴CF=OF=1;
又∵AD、AF是⊙O的切线,
∴AF=AD;
∴AF=AC-CF=AC-OF=4-1=3,即AD=3);
(2)如图1,若点P在线段AC上时.
在Rt△ABC中,AB=5,AC=4,BC=3,
∵∠C=90°,PH⊥AB,
∴∠C=∠PHA=90°,
∵∠A=∠A,
∴△AHP∽△ACB,
∴$\frac{PH}{BC}$=$\frac{AP}{AB}$=$\frac{AC-PC}{AB}$,即$\frac{x}{3}$=$\frac{4-y}{5}$,
∴y=-$\frac{5}{3}$x+4,即y与x的函数关系式是y=-$\frac{5}{3}$x+4(0≤x≤2.4);
(3)①当点P在线段AC上时,如图2,P′H′与⊙O相切.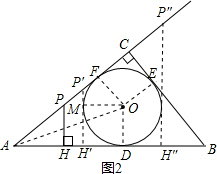
∵∠OMH′=∠MH′D=∠H′DO=90°,OM=OD,
∴四边形OMH′D是正方形,
∴MH′=OM=1;
由(1)知,四边形CFOE是正方形,
CF=OF=1,
∴P′H′=P′M+MH′=P′F+FC=P′C,即x=y;
又由(2)知,y=-$\frac{5}{3}$x+4,
∴y=-$\frac{5}{3}$y+4,
解得y=$\frac{3}{2}$;
②同(2),当点P在线段AC的延长线上时,△AHP∽△ACB,
则$\frac{PH}{BC}$=$\frac{AP}{AB}$=$\frac{AC+PC}{AB}$,即$\frac{x}{3}$=$\frac{4+y}{5}$,
∴y=$\frac{5}{3}$x-4,即y与x的函数关系式是y=$\frac{5}{3}$x-4(x>2.4);
如图2,当P″H″与⊙O相切时,同①可求得y=1;
综上可知PC的值为$\frac{3}{2}$或1.
点评 本题主要考查了圆的综合题,涉及相似三角形的判定与性质、三角形的内切圆等知识点.在(2)中注意分两种情况进行讨论,通过做此题培养了学生的推理能力,此题综合性比较强,有一定的难度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
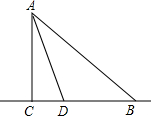 如图,在Rt△ACB中,∠ACB=90°,AC=BC=12,D为边BC上一点,CD=4,K为直线BC上一点,∠DAK=45°,则CK的长为24或6.
如图,在Rt△ACB中,∠ACB=90°,AC=BC=12,D为边BC上一点,CD=4,K为直线BC上一点,∠DAK=45°,则CK的长为24或6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
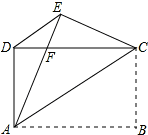 如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
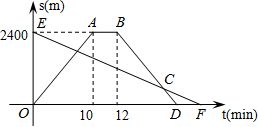 小明早8点从家骑自行车出发,沿一条直路去邮局办事,小明出发的同时,他的爸爸从邮局沿同一条道路步行回家,小明在邮局停留了一会后沿原路以原速度返回,小明比爸爸早3分钟到家.设他们与家的距离S(m)与离开家的时间t(min)之间函数关系的如图所示,有下列说法:①邮局与家的距离为2400米;②小明到家的时间为8:22分;③爸爸的速度为96mAmin;④小明在返回途中离家480米处于爸爸相遇,其中正确的说法有( )
小明早8点从家骑自行车出发,沿一条直路去邮局办事,小明出发的同时,他的爸爸从邮局沿同一条道路步行回家,小明在邮局停留了一会后沿原路以原速度返回,小明比爸爸早3分钟到家.设他们与家的距离S(m)与离开家的时间t(min)之间函数关系的如图所示,有下列说法:①邮局与家的距离为2400米;②小明到家的时间为8:22分;③爸爸的速度为96mAmin;④小明在返回途中离家480米处于爸爸相遇,其中正确的说法有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com