
【题目】回答下列问题
(1)问题发现 如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,求∠AEB的度数.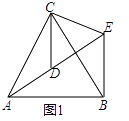
(2)拓展探究 如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.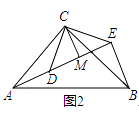
【答案】
(1)解:∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=60°﹣∠CDB=∠BCE.
在△ACD和△BCE中,
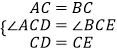 ,
,
∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°,
∴∠BEC=120°.
∴∠AEB=∠BEC﹣∠CED=60°
(2)解:∠AEB=90°,AE=BE+2CM.
理由:∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
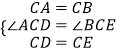 ,
,
∴△ACD≌△BCE(SAS).
∴AD=BE,∠ADC=∠BEC.
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,
∴∠ADC=135°,
∴∠BEC=135°.
∴∠AEB=∠BEC﹣∠CED=90°.
∵CD=CE,CM⊥DE,
∴DM=ME.
∵∠DCE=90°,
∴DM=ME=CM.
∴AE=AD+DE=BE+2CM
【解析】(1)先证出∠ACD=∠BCE,那么△ACD≌△BCE,根据全等三角形证出∠ADC=∠BEC,求出∠ADC=120°,得出∠BEC=120°,从而证出∠AEB=60°;(2)证明△ACD≌△BCE,得出∠ADC=∠BEC,最后证出DM=ME=CM即可.
【考点精析】利用等边三角形的性质对题目进行判断即可得到答案,需要熟知等边三角形的三个角都相等并且每个角都是60°.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】【阅读】
我们分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,
其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M﹣N,若M﹣N>0,则M>N;若M﹣N=0,则M=N;若M﹣N<0,则M<N.
【运用】
利用“作差法”解决下列问题:
(1)小丽和小颖分别两次购买同一种商品,小丽两次都买了m千克商品,小颖两次购买商品均花费n元,已知第一次购买该商品的价格为a元/千克,第二次购买该商品的价格为b元/千克(a,b是整数,且a≠b),试比较小丽和小颖两次所购买商品的平均价格的高低.
(2)奶奶提一篮子玉米到集贸市场去兑换大米,每2kg玉米兑换1kg大米,商贩用秤称得连篮子带玉米恰好20kg,于是商贩连篮子带大米给奶奶共10kg,在这个过程中谁吃了亏?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图梯形ABCD中,AD∥BC,∠ABC+∠C=90°,AB=6,CD=8,M,N,P分别为AD、BC、BD的中点,则MN的长为( ) 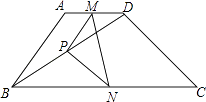
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
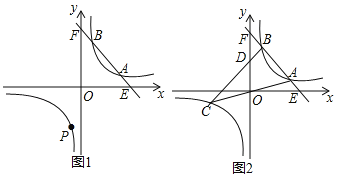
【题目】已知:一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() )的图象相交于A,B两点(A在B的右侧).
)的图象相交于A,B两点(A在B的右侧).
(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;
(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠A=55°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( ) 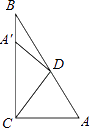
A.40°
B.30°
C.20°
D.10°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅在架设电线时,为了检验三条电线是否互相平行只检查了其中两条是否与第三条平行即可,这样做的道理是______________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com