
����Ŀ�����Ķ���
���Ƿ������ijЩ��ѧ����ʱ������Ҫ�Ƚ������������ʽ�Ĵ�С�����������IJ���һ��Ҫ����һ����ת����
���С���������dz��õķ���֮һ����ν�������������ͨ��������Σ������ò�ķ���ȷ�����ǵĴ�С����Ҫ�Ƚϴ���ʽM��N�Ĵ�С��ֻҪ�������ǵIJ�M��N����M��N��0����M��N����M��N=0����M=N����M��N��0����M��N��
�����á�
���á����������������⣺
��1��С����Сӱ�ֱ����ι���ͬһ����Ʒ��С�����ζ�����mǧ����Ʒ��Сӱ���ι�����Ʒ������nԪ����֪��һ�ι������Ʒ�ļ۸�ΪaԪ/ǧ�ˣ��ڶ��ι������Ʒ�ļ۸�ΪbԪ/ǧ�ˣ�a��b����������a��b�����ԱȽ�С����Сӱ������������Ʒ��ƽ���۸�ĸߵͣ�
��2��������һ����������ó�г�ȥ�һ����ף�ÿ2kg���һ�1kg���ף��̷��óӳƵ������Ӵ�����ǡ��20kg�������̷������Ӵ��������̹�10kg�������������˭���˿�����˵�����ɣ�
���𰸡��⣺��1����![]() =
=![]() ��
��![]() =
=![]() ��
��
��![]() ��
��![]() =
=![]() =
=![]() ��0��
��0��
��С��������������Ʒ��ƽ���۸�ߣ�
��2�����̳Կ���
���ɣ���������xkg�������أ�20��x��kg��
Ӧ��ȡ![]() kg���ף�
kg���ף�
�̷������̵Ĵ��ף�10��x��kg��![]() ����10��x��=
����10��x��=![]() ��
��
���ڴ˹��������̳Կ����Կ�![]() ǧ�ˣ�
ǧ�ˣ�
����������1����������ֱ��ʾ��С����Сӱ������������Ʒ��ƽ���۸���������Ƚϼ��ɣ�
��2�������ӵ�����Ϊxkg����������ɵ������е���������Ϊ��20��x��kg��С����С���Ĵ�������Ϊ��10��![]() ��kg���ٸ������״��һ��������ɵý⣮
��kg���ٸ������״��һ��������ɵý⣮
�����㾫�������շ�ʽ��ֵ�ǽ����ĸ�������Ҫ֪��һ����ʽ�ķ��ӡ���ĸ���ʽ�����ķ��ţ��ı������κ���������ʽ��ֵ���䣮


 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
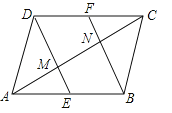
����Ŀ����ͼ����ABCD�У�E��F�ֱ���AB��CD���е㣮
��1����֤���ı���EBFDΪƽ���ı��Σ�
��2���Խ���AC�ֱ���DE��BF���ڵ�M��N����֤����ABN�ա�CDM��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
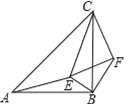
����Ŀ����ͼ����ABC�͡�CEF��Ϊ����ֱ�������Σ�E�ڡ�ABC�ڣ���CAE+��CBE=90�㣬����BF��
��1����֤����CAE�ס�CBF��
��2����BE=1��AE=2����CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ȱߡ�ABC�߳�Ϊ1cm��D��E�ֱ���AB��AC�����㣬����ADE��ֱ��DE�۵�����A����A������A�ڡ�ABC�⣬����Ӱ����ͼ���ܳ�Ϊ�� �� 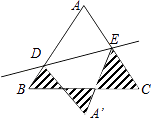
A.1cm
B.1.5cm
C.2cm
D.3cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABC��AC=BC����ACB=90�㣬ADΪ��ƽ���ߣ��ӳ�AD��BF��E��EΪBF�е㣬���н��۴�����ǣ� �� 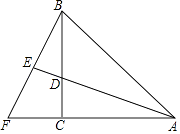
A.AD=BF
B.CF=CD
C.AC+CD=AB
D.BE=CF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У���֪AD��AB��
��1��ʵ�������������BAD��ƽ���߽�BC�ڵ�E����AD�Ͻ�ȡAF=AB������EF����Ҫ�߹���ͼ��������ͼ�ۼ�����д������
��2�����벢֤���������ı���ABEF����״��������֤����
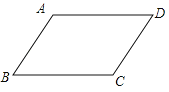
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������е��ĸ���֮�䶼��һ���Ĺ��ɣ����˹��ɵó�a��b��ֵ�ֱ�Ϊ�� ��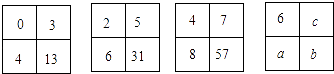
A.9��10
B.9��91
C.10��91
D.10��110
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��Ե�B��0��8��Ϊ�˵������BG��x�ᣬ��A������BG�ϵ�һ�����㣨��A���B���غϣ���������AG��ȡAD=OB�����߶�AD�Ĵ�ֱƽ���ߣ�����ΪE������x�ύ�ڵ�F������A��AC��OA��������EF�ڵ�C������OC��CD�����A�ĺ�����Ϊt��
��1���ú�t��ʽ�ӱ�ʾ��E������Ϊ_______��
��2����tΪ��ֵʱ����OCD=180����
��3������C���F���غ�ʱ������OCF�����ΪS����S��t֮��ĺ�������ʽ��
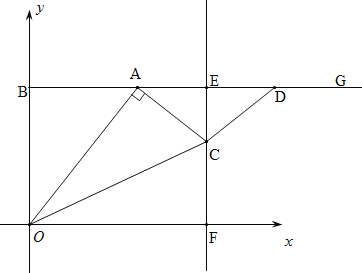
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com