
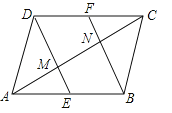
【题目】如图,在ABCD中,E、F分别是AB、CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE、BF交于点M、N,求证:△ABN≌△CDM.
【答案】(1)证明见试题解析;(2)证明见试题解析.
【解析】
试题分析:(1)根据平行四边形的性质,得到AB∥CD,AB=CD;再根据一组对边平行且相等的四边形是平行四边形,可得答案;
(2)根据平行四边的性质,可得AB∥CD,AB=CD,∠CDM=∠CFN;根据全等三角形的判定,可得答案.
试题解析:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∵E、F分别是AB、CD的中点,∴BE=DF,∵BE∥DF,∴四边形EBFD为平行四边形;
(2)∵四边形EBFD为平行四边形,∴DE∥BF,∴∠CDM=∠CFN,∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∴∠BAC=∠DCA,∠ABN=∠CFN,∴∠ABN=∠CDM,在△ABN与△CDM中,∵∠BAN=∠DCM,AB=CD,∠ABN=∠CDM,∴△ABN≌△CDM (ASA).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正比例函数y=kx(k>0)与反比例函数y= ![]() 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为(m , 0).其中m>0.
的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为(m , 0).其中m>0.
(1)四边形ABCD的是 . (填写四边形ABCD的形状)
(2)当点A的坐标为(n,3)时,四边形ABCD是矩形,求mn的值.
(3)试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知互不相等的实数m、n,且满足m2+3m﹣5=0,n2+3n﹣5=0,则m2﹣n2+mn+6m的值为( )
A.14B.﹣14C.10D.﹣10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论
①△ADC≌△ADE;
②CE平分∠DEF;
③AD垂直平分CE.
其中正确的个数有( )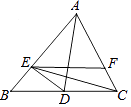
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
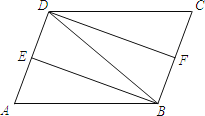
【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅不完整的统计图,请根据图中信息,解答下列问题: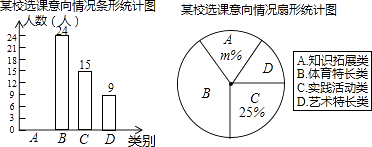
(1)求扇形统计图中m的值;
(2)补全条形统计图;
(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排20人,问学校开设多少个“实践活动类”课程的班级比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读】
我们分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,
其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M﹣N,若M﹣N>0,则M>N;若M﹣N=0,则M=N;若M﹣N<0,则M<N.
【运用】
利用“作差法”解决下列问题:
(1)小丽和小颖分别两次购买同一种商品,小丽两次都买了m千克商品,小颖两次购买商品均花费n元,已知第一次购买该商品的价格为a元/千克,第二次购买该商品的价格为b元/千克(a,b是整数,且a≠b),试比较小丽和小颖两次所购买商品的平均价格的高低.
(2)奶奶提一篮子玉米到集贸市场去兑换大米,每2kg玉米兑换1kg大米,商贩用秤称得连篮子带玉米恰好20kg,于是商贩连篮子带大米给奶奶共10kg,在这个过程中谁吃了亏?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com