
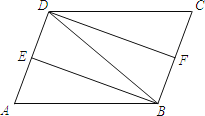
【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据平行四边形性质得出AB=CD,∠A=∠C.求出∠ABD=∠CDB.推出∠ABE=∠CDF,根据ASA推出全等即可;
(2)根据全等得出AE=CF,根据平行四边形性质得出AD∥BC,AD=BC,推出DE∥BF,DE=BF,得出四边形DFBE是平行四边形,根据等腰三角形性质得出∠DEB=90°,根据矩形的判定推出即可.
试题解析:(1)在□ABCD中,AB=CD,∠A=∠C.∵AB∥CD,∴∠ABD=∠CDB.
∵BE平分∠ABD,DF平分∠CDB,∴∠ABE=![]() ∠ABD,∠CDF=
∠ABD,∠CDF=![]() ∠CDB,∴∠ABE=∠CDF.
∠CDB,∴∠ABE=∠CDF.
∵在△ABE和△CDF中,∵∠A=∠C,AB=DC,∠ABE=∠CDF,∴△ABE≌△CDF(ASA).
(2)∵△ABE≌△CDF,∴AE=CF,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴DE∥BF,DE=BF,∴四边形DFBE是平行四边形,∵AB=DB,BE平分∠ABD,∴BE⊥AD,即∠DEB=90°,∴平行四边形DFBE是矩形.


科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线 ![]() 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且
与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 ![]() ,则k的值是( )
,则k的值是( )
A.4
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个等边三角形木框,甲虫P在边框AC上爬行(A,C端点除外),设甲虫P到另外两边的距离之和为d,等边三角形ABC的高为h,则d与h的大小关系是( ) 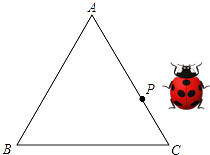
A.d>h
B.d<h
C.d=h
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
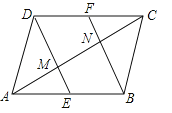
【题目】如图,在ABCD中,E、F分别是AB、CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE、BF交于点M、N,求证:△ABN≌△CDM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司今年元月份利润为500万元,以后两个月均匀增长,第一季度的利润1820万元,设该公司利润月平均增长率为x,根据题意可列方程_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车队要把4000吨货物运到雅安地震灾区(方案定后,每天的运量不变)。
(1)从运输开始,每天运输的货物吨数n(单位:吨)与运输时间t(单位:天)之间有怎样的函数关系式?
(2)因地震,到灾区的道路受阻,实际每天比原计划少运20%,则推迟1天完成任务,求原计划完成任务的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC,AC=BC,∠ACB=90°,AD为角平分线,延长AD交BF于E,E为BF中点,下列结论错误的是( ) 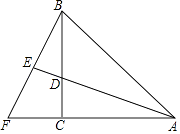
A.AD=BF
B.CF=CD
C.AC+CD=AB
D.BE=CF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com