
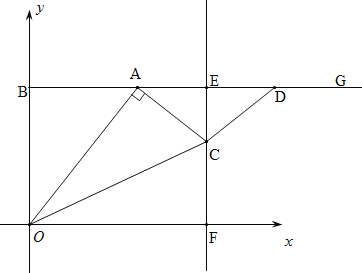
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��Ե�B��0��8��Ϊ�˵������BG��x�ᣬ��A������BG�ϵ�һ�����㣨��A���B���غϣ���������AG��ȡAD=OB�����߶�AD�Ĵ�ֱƽ���ߣ�����ΪE������x�ύ�ڵ�F������A��AC��OA��������EF�ڵ�C������OC��CD�����A�ĺ�����Ϊt��
��1���ú�t��ʽ�ӱ�ʾ��E������Ϊ_______��
��2����tΪ��ֵʱ����OCD=180����
��3������C���F���غ�ʱ������OCF�����ΪS����S��t֮��ĺ�������ʽ��
���𰸡���1��E��![]() ��8������2��
��8������2��![]() ����3��
����3��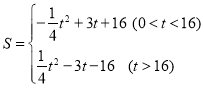 ��
��
��������
�����������1����AD=OB=8���õ�AE=ED=4�����ɵ�A�ĺ�����Ϊt���õ���E�����ꣻ
��2������OCD=180��ʱ����ͼ1����EC��BO���õ�![]() ����EC=
����EC=![]() ��������AEC�ס�OBA���õ�
��������AEC�ס�OBA���õ�![]() ���Ӷ�EC=
���Ӷ�EC=![]() ����
����![]() =
=![]() ���ⷽ�̼������t��ֵ��
���ⷽ�̼������t��ֵ��
��3����C��F�غ�ʱ���ɣ�2���ã�![]() =8�����t=16���ʷ�����������ۣ���
=8�����t=16���ʷ�����������ۣ���![]() ����
����![]() ������
������![]() ��OF=BE=
��OF=BE=![]() ��ֻ��Ҫ��ʾ��CF���빫ʽ���ɣ�
��ֻ��Ҫ��ʾ��CF���빫ʽ���ɣ�
�����������1����AD=OB=8����AE=ED=4������A�ĺ�����Ϊt����E��![]() ��8����
��8����
��2������OCD=180��ʱ����ͼ1����EC��BO����![]() ����
����![]() ����EC=
����EC=![]() ����AC��OA�����1+��2=90�����ߡ�2+��3=90�������1=��3���ߡ�AEC=��ABO�����AEC�ס�OBA����
����AC��OA�����1+��2=90�����ߡ�2+��3=90�������1=��3���ߡ�AEC=��ABO�����AEC�ס�OBA����![]() ����
����![]() ����EC=
����EC=![]() ����
����![]() =
=![]() ����
����![]() ����ã�
����ã�![]() ��
��![]() ����ȥ������t=
����ȥ������t=![]() ��
��

��3����C��F�غ�ʱ���ɣ�2���ã�![]() =8�����t=16����������������ۣ���
=8�����t=16����������������ۣ���![]() ����
����![]() ��
��
����![]() ʱ����ͼ2���ɣ�2���ã�EC=
ʱ����ͼ2���ɣ�2���ã�EC=![]() ����CF=
����CF=![]() ����OF=BE=
����OF=BE=![]() ����
����![]() ����
����![]() ��
��
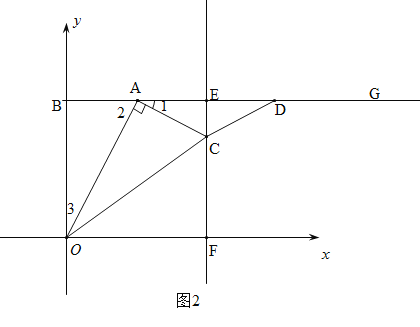
����![]() ʱ����ͼ3���ɣ�2���ã�EC=
ʱ����ͼ3���ɣ�2���ã�EC=![]() ����CF=
����CF=![]() ����OF=BE=
����OF=BE=![]() ��
��
��![]() ����
����![]() ��
��

����������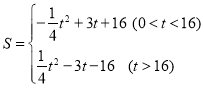 ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC����A1B1C1���ƣ������Ʊ�Ϊ1��3������ABC����A1B1C1���ܳ���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ���
���Ƿ������ijЩ��ѧ����ʱ������Ҫ�Ƚ������������ʽ�Ĵ�С�����������IJ���һ��Ҫ����һ����ת����
���С���������dz��õķ���֮һ����ν�������������ͨ��������Σ������ò�ķ���ȷ�����ǵĴ�С����Ҫ�Ƚϴ���ʽM��N�Ĵ�С��ֻҪ�������ǵIJ�M��N����M��N��0����M��N����M��N=0����M=N����M��N��0����M��N��
�����á�
���á����������������⣺
��1��С����Сӱ�ֱ����ι���ͬһ����Ʒ��С�����ζ�����mǧ����Ʒ��Сӱ���ι�����Ʒ������nԪ����֪��һ�ι������Ʒ�ļ۸�ΪaԪ/ǧ�ˣ��ڶ��ι������Ʒ�ļ۸�ΪbԪ/ǧ�ˣ�a��b����������a��b�����ԱȽ�С����Сӱ������������Ʒ��ƽ���۸�ĸߵͣ�
��2��������һ����������ó�г�ȥ�һ����ף�ÿ2kg���һ�1kg���ף��̷��óӳƵ������Ӵ�����ǡ��20kg�������̷������Ӵ��������̹�10kg�������������˭���˿�����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
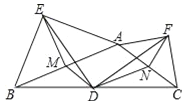
����Ŀ����ͼ���ڶ۽ǡ�ABC�У���D��BC���е㣬�ֱ���AB��ACΪб�����ABC�����������ֱ��������ABE�͵���ֱ��������ACF��M��N�ֱ�ΪAB��AC���е㣬����DM��DN��DE��DF��EM��EF��FN����֤��
��1����EMD�ա�DNF��
��2����EMD�ס�EAF��
��3��DE��DF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ��⣺̽�����ֹ�����չӦ����
��1����ͼ�٣���CEF=90�㣬��B������EF�ϣ�AB��CD������ABE=130�㣬���C�Ķ�����
��2����ͼ�ڣ��ѡ���CEF=90�㡱��Ϊ����CEF=120�㡱����B������EF�ϣ�AB��CD�������ABE���C��������ϵ����˵�����ɣ�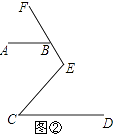
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��˳���������θ��ߵ��е����γɵ��ı����ǣ� ��
A.��������
B.����
C.����
D.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪DE��BC��CD�ǡ�ACB��ƽ���ߣ���B=70�㣬��ACB=50�㣬���EDC�͡�BDC�Ķ����� 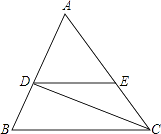
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���C=90�㣬D��E��F�ֱ�ΪAB��BC��AC���ϵ��е㣬AC=4cm��BC=6cm����ô�ı���CEDFΪ �� ���ı߳��ֱ�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y��3x2������ƽ��1����λ���ȣ�������ƽ��4����λ���ȣ�ƽ�ƺ������ߵĺ�������ʽ��(����)
A. y��3(x+1)2+4B. y��3(x��1)2+4
C. y��3(x+1)2��4D. y��3(x��1)2��4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com