
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,若∠ABC=30°,∠C=45°,ED=![]() ,点H是BD上的一个动点,则HG+HC的最小值为______________.
,点H是BD上的一个动点,则HG+HC的最小值为______________.

【答案】![]()
【解析】
首先证明四边形BEDG是菱形,作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在Rt△EMC中,求出EM、MC即可解决问题.
解:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
在△EFD和△GFB中,
∴△EFD≌△GFB(AAS)
∴ED=BG,
∴BE=ED=DG=GB,
∴四边形EBGD是菱形.
如图,作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小
在Rt△EBM中,∵∠EMB=90°,∠EBM=30°,EB=ED=2![]()
![]() ,
,
∴EM=![]() BE=
BE=![]() ,
,
∵DE∥BC,EM⊥BC,DN⊥BC,
∴EM∥DN,EM=DN=![]() ,MN=DE=2
,MN=DE=2![]() ,
,
在Rt△DNC中,∵∠DNC=90°,∠DCN=45°,
∴∠NDC=∠NCD=45°,
∴DN=NC=![]() ,
,
∴MC=3![]() ,
,
在Rt△EMC中,∵∠EMC=90°,EM=![]() .MC=3
.MC=3![]() ,
,
∴EC=![]() =5
=5![]() .
.
∵HG+HC=EH+HC=EC,
∴HG+HC的最小值为5![]() .
.
故答案为5![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,∠MON![]() 60°,点A是OM边上一点,点B,C是ON边上两点,且AB
60°,点A是OM边上一点,点B,C是ON边上两点,且AB![]() AC,作点B关于OM的对称点点D,连接AD,CD,OD.
AC,作点B关于OM的对称点点D,连接AD,CD,OD.
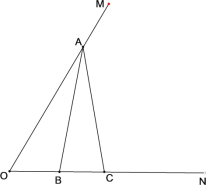

(1)依题意补全图形;
(2)猜想∠DAC![]() °,并证明;
°,并证明;
(3)猜想线段OA、OD、OC的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法:①四个角都相等的四边形是矩形;②有一组对边平行,有两个角为直角的四边形是矩形;③两组对边分别相等且有一个角为直角的四边形是矩形;④对角线相等且有一个角是直角的四边形是矩形;⑤对角线互相平分且相等的四边形是矩形.其中,正确的个数是( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图:

![]()
(1)该班总人数是 ;
(2)根据计算,请你补全两个统计图;
(3)观察补全后的统计图,写出一条你发现的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.
ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.

(1)求证:△ADE≌△BFE;
(2)若DF平分∠ADC,连接CE.试判断CE和DF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表.设分配给甲店A型产品![]() 件,这家公司卖出这100件产品的总利润为W(元).
件,这家公司卖出这100件产品的总利润为W(元).

(1)求W关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围;
的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案?
(3)实际销售过程中,公司发现这批产品尤其是A型产品很畅销,便决定对甲店的最后21件A型产品每件提价![]() 元销售(
元销售(![]() 为正整数).两店全部销售完毕后结果的总利润为18000元,求
为正整数).两店全部销售完毕后结果的总利润为18000元,求![]() 值.并写出公司这100件产品对甲乙两店是如何分配的?
值.并写出公司这100件产品对甲乙两店是如何分配的?
查看答案和解析>>
科目:初中数学 来源: 题型:
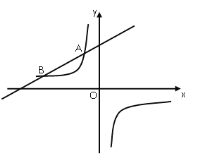
【题目】如图,一次函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像与反比例函数
)的图像与反比例函数![]() 的图像交于
的图像交于![]() ,
,![]() 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线![]() 向下平移
向下平移![]() 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过对《勾股定理》的学习,我们知道:如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.如果我们新定义一种三角形——两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗?
(填“是”或不是);
(2)若某三角形的三边长分别为1、![]() 、2,则该三角形是不是奇异三角形,请做出判断并写出判断依据;
、2,则该三角形是不是奇异三角形,请做出判断并写出判断依据;
(3)在![]() 中,两边长分别为
中,两边长分别为![]() ,且且
,且且![]() ,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;
,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;
探究:Rt![]() 中,
中,![]() ,且b>a,若Rt
,且b>a,若Rt![]() 是奇异三角形,求
是奇异三角形,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程k2x2﹣2(k+1)x+1=0有两个实数根.
(1)求k的取值范围;
(2)当k=1时,设所给方程的两个根分别为x1和x2,求(x1﹣2)(x2﹣2)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com