
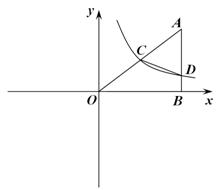
如图,在平面直角坐标系中A点的坐标为(8,y) ,AB⊥x轴于点B, sin∠OAB = 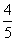 ,反比例函数y =
,反比例函数y = 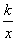 的图象的一支经过AO的中点C,且与AB交于点D.【版权所有:21教育】
的图象的一支经过AO的中点C,且与AB交于点D.【版权所有:21教育】
(1)求反比例函数解析式;
(2)若函数y = 3x 与y = 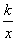 的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.
的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:
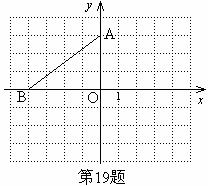 在平面直角坐标系中,点A的坐标是(0,3),点B在
在平面直角坐标系中,点A的坐标是(0,3),点B在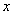 轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F。21·世纪*教育网
轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F。21·世纪*教育网
(1)若点B的坐标是(-4,0),请在图中画出
△AEF,并写出点E,F的坐标;
(2)当点F落在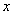 轴上方时,试写出一个符合条件的点B的坐标。
轴上方时,试写出一个符合条件的点B的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图, 
 ABCD的对角线AC、BD相交于点O,AE=CF.
ABCD的对角线AC、BD相交于点O,AE=CF.
(1)求证:△BOE ≌△DOF ;
(2)若BD=EF,连接DE、BF,判断四边形EBFD的形状,无需说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
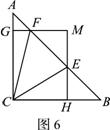
如图6,在△ABC中,∠ACB=90º,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=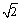 ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=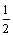 ;③AF+BE=EF;④MG•MH=
;③AF+BE=EF;④MG•MH=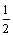 ,其中正确结论为
,其中正确结论为
A.①②③ B.①③④
C.①②④ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
某小组5名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是21·cn·jy·com
| 劳动时间(小时) | 3 | 3.5 | 4 | 4.5 |
| 人 数 | 1 | 1 | 2 | 1 |
A.中位数是4,平均数是3.75 B.众数是4,平均数是3.75
C.中位数是4,平均数是3.8 D.众数是2,平均数是3.8
查看答案和解析>>
科目:初中数学 来源: 题型:
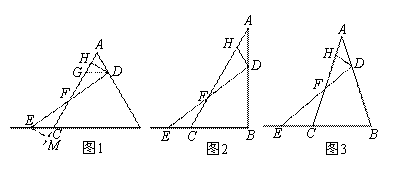
问题背景:已知在△ABC中,AB边上的动点D由A向B运动(与A,B不重合),点E与点D同时出发,由点C沿BC的延长线方向运动(E不与C重合),连结DE交AC于点F,点H是线段AF上一点
1) 初步尝试:如图1,若△ABC是等边三角形,DH⊥AC,且点D,E的运动速度相等,求证:HF=AH+CF
小王同学发现可以由 以下两种思路解决此问题:
以下两种思路解决此问题:
思路一:过点D作D G∥BC,交AC于点G,先证GH=AH,再证GF=CF,从而证得结论成立
G∥BC,交AC于点G,先证GH=AH,再证GF=CF,从而证得结论成立
思路二:过点E作EM⊥AC,交AC的延长线于点M,先证CM=AH,再证HF=MF,从而证得结论成立
请 你任选一种思路,完整地书写本小题的证明过
你任选一种思路,完整地书写本小题的证明过 程(如用两种方法作答,则以第一种方法评分)
程(如用两种方法作答,则以第一种方法评分)
2) 类比探究:如图2,若在△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且点D,E的运动速度之比是 :1,求
:1,求 的值
的值
3) 延伸拓展:如图3,若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记 =m,且点D、E的运动速度相等,试用含m的代数式表示
=m,且点D、E的运动速度相等,试用含m的代数式表示 (直接写出结果,不必写解答过程)
(直接写出结果,不必写解答过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com