
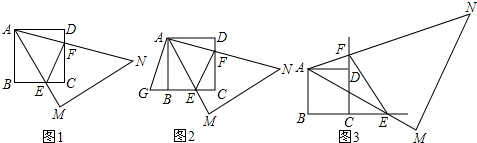
分析 (1)根据正方形性质得出AD=AB,∠D=∠ABG,根据全等三角形的判定推出即可;
(2)①EF=BE-DF,理由是:在BC上取BG=DF,连接AG,证△ABG≌△ADF,△FAE≌△EAG即可;
②设正方形ABCD的边长是x,则BC=CD=x,EF=GE=BC-BG+CE=x+4,在Rt△FCE中,由勾股定理得出方程(x+4)2=(x+2)2+62,求出即可.
解答 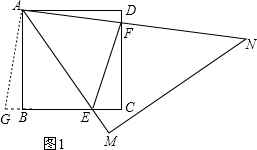 (1)证明:①如图1,延长CB到G,使BG=DF,连接AG,
(1)证明:①如图1,延长CB到G,使BG=DF,连接AG,
∵四边形ABCD是正方形,
∴∠D=∠ABC=∠DAB=∠ABG=90°,AD=AB,
在△ADF和△ABG中,
$\left\{\begin{array}{l}{AD=AB}\\{∠D=∠ABG}\\{DF=BG}\end{array}\right.$,
∴△ADF≌△ABG(SAS);
(2)①不成立,三线段EF、DF、BE的数量关系是EF=BE-DF,
证明:如图3,在BC上取BG=DF,连接AG,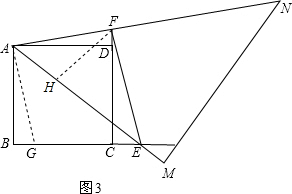
在△ABG和△ADF中
$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠ADF}\\{BG=DF}\end{array}\right.$
∴△ABG≌△ADF(SAS),
∴AF=AG,∠DAF=∠BAG,
∵△AMN是等腰直角三角形,
∴∠NAM=∠N=45°,
∴∠FAD+∠DAC=45°,
∴∠DAC+∠BAG=45°,
∵∠DAB=90°,
∴∠GAE=90°-45°=45°=∠FAE,
在△FAE和△GAE中
$\left\{\begin{array}{l}{AF=AG}\\{∠FAE=GAF}\\{AE=AE}\end{array}\right.$
∴△FAE≌△GAE(SAS),
∴EF=EG=BE-BG,
∵BG=DF,
∴EF=BE-DF.
②解:设正方形ABCD的边长是x,则BC=CD=x,
∵CE=6,DF=BG=2,
∴EF=GE=CG+CE=BC-BG+CE=x-2+6=x+4,
在Rt△FCE中,由勾股定理得:EF2=FC2+CE2,
∴(x+4)2=(x+2)2+62,
解得:x=6,
∴AG=AF=$\sqrt{36+4}=2\sqrt{10}$,
∵∠FAM=45°,
如图3,过F作FH⊥AE于H,
∴FH=$\frac{{\sqrt{2}}}{2}$AF,
=$\frac{{\sqrt{2}}}{2}×2\sqrt{10}$
=$2\sqrt{5}$,
即△AEF中AE边上的高为$2\sqrt{5}$.
点评 本题考查了全等三角形的性质和判定,正方形的性质,勾股定理的应用,主要考查学生的推理能力,证明过程类似.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:解答题
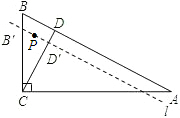 如图,在Rt△ABC中,∠ACB=90°,AC=$6\sqrt{3}$cm,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=$6\sqrt{3}$cm,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
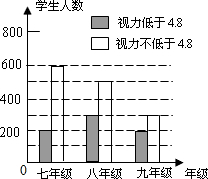 某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图如图所示,则下列说法中不正确的是( )
某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图如图所示,则下列说法中不正确的是( )| A. | 本次抽查活动共抽查了2100名学生 | |
| B. | 本次抽查活动中视力不低于4.8的学生人数占总人数的66.7% | |
| C. | 本次抽查活动中视力不低于4.8学生人数中的极差为300人 | |
| D. | 由活动结果可以知道随着年级的增长,视力低于4.8的人数越来越多,呈上升趋势,那么同年级中抽到视力不低于4.8的学生的概率将越来越小 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
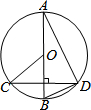 如图所示,AB为⊙O的直径,CD为弦,AB⊥CD,如果∠BOC=50°,那么∠ABD的度数为( )
如图所示,AB为⊙O的直径,CD为弦,AB⊥CD,如果∠BOC=50°,那么∠ABD的度数为( )| A. | 25° | B. | 20° | C. | 65° | D. | 50° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com