练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

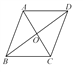
    【题目】已知如图所示，△AOB与△COD关于点O成中心对称，连接BC，AD.

    (1)求证：四边形ABCD为平行四边形；

    (2)若△AOB的面积为15 cm2，求四边形ABCD的面积.

    【答案】（1）证明见解析；（2）60 cm2.

    【解析】试题分析：根据成中心对称图形的性质知OA=OC，OB=OD.根据平行四边形对角线互相平分，所以可以得到四边形ABCD为平行四边形；△AOB的面积为15 cm2，则△ABC面积等于△AOB面积的2倍，因为点O为平行四边形的中心，所以△ABC的高等于△AOB高的2倍，所以S△ABC =30，所以四边形ABCD的面积是60.

    (1)∵AOB与△COD关于点O成中心对称，∴OA=OC，OB=OD.

    ∴四边形ABCD为平行四边形.

    (2)四边形ABCD的面积为60 cm2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】列方程解应用题：

    中华优秀传统文化是中华民族的“根”和“魂”，是我们必须世代传承的文化根脉、文化基因.为传承优秀传统文化，某校为各班购进《三国演义》和《水浒传》连环画若干套，其中每套《三国演义》连环画的价格比每套《水浒传》连环画的价格贵60元，用4800元购买《水浒传》连环画的套数是用3600元购买《三国演义》连环画套数的2倍，求每套《水浒传》连环画的价格．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】全民健身和医疗保健是社会普遍关注的问题.2014年，某社区共投入30万元用于购买健身器材和药品.2015年，该社区购买健身器材的费用比上一年增加50%，购买药品的费用比上一年减少，但社区在这两方面的总投入仍与2014年相同．

    (1)求2014年社区购买药品的总费用；

    (2)据统计，2014年该社区积极健身的家庭达到200户，但其药品费用明显减少，只占当年购买药品总费用的.与2014年相比，如果2015年社区内健身家庭户数增加的百分数与平均每户健身家庭的药品费用降低的百分数相同，那么，2015年该社区用于健身家庭的药品费用就是当年购买健身器材费用的.求2015年该社区健身家庭的户数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解题：

    定义：如果一个数的平方等于-1，记为i2=-1，这个数i叫做虚数单位．那么和我们所学的实数对应起来就叫做复数，表示为a+bi（a，b为实数），a叫这个复数的实部，b叫做这个复数的虚部，它的加，减，乘法运算与整式的加，减，乘法运算类似．

    例如计算：（5+i）×（3-4i）=19-17i．

    （1）填空：i3= ，i4= .

    （2）计算：（3+i）2；

    （3）试一试：请利用以前学习的有关知识将化简成a+bi的形式

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，并完成填空．

    你能比较20152 016和20162 015的大小吗？

    为了解决这个问题，先把问题一般化，比较nn＋1和(n＋1)n(n≥1，且n为整数)的大小．然后从分析n＝1，n＝2，n＝3…的简单情形入手，从中发现规律，经过归纳、猜想得出结论．

    (1)通过计算(可用计算器)比较下列①～⑦组两数的大小：(在横线上填上“>”“＝”或“<”)

    ①12____21；②23_____32；③34_____43；④45_____54；

    ⑤56____65；⑥67_____76；⑦78_____87；

    (2)归纳第(1)问的结果，可以猜想出nn＋1和(n＋1)n的大小关系；

    (3)根据以上结论，可以得出20162017和20172016的大小关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．

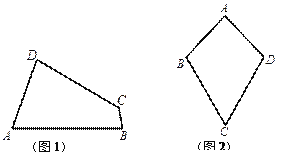
    （1）已知：如图1，四边形是“等对角四边形”， ， ， ．求， 的度数．

    （2）在探究“等对角四边形”性质时：

    ① 小红画了一个“等对角四边形”（如图2），其中， ，此时她发现成立．请你证明此结论．

    ② 由此小红猜想：“对于任意‘等对角四边形’，当一组邻边相等时，另一组邻边也相等”．你认为她的猜想正确吗？若正确，请证明；若不正确，请举出反例．

    （3）已知：在“等对角四边形”中， ， ，AB=AD=4，．求∠D和对角线的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】矩形纸片ABCD中，已知AD=8，AB=6，E是边BC上的点，以AE为折痕折叠纸片，使点B落在点F处，连接FC，当△EFC为直角三角形时，BE的长为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

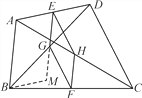
    【题目】在四边形ABCD中，E、F分别是AD、BC的中点，G、H分别是BD、AC的中点，当AB、CD满足什么条件时，四边形EGFH是菱形？请证明你的结论．(提示：过点B作BM∥AD交EG的延长线于点M，证明EG//AB且EG=AB)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E、F，给出的以下四个结论：①AE=CF； ②△EPF一定是等腰直角三角形； ③S四边形AEPF=S△ABC；④当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP。（点E不与A、B重合），上述结论中始终正确的有_____.（写序号）

    查看答案和解析>>

    同步练习册答案