Question

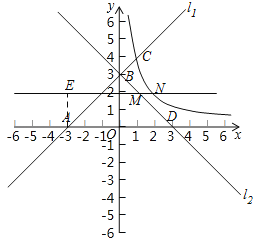
【题目】已知直线l1：y=x+3与x轴交于点A，与y轴交于点B，且与双曲线交于点C（1，a）．

（1）试确定双曲线的函数表达式；

（2）将l1沿y轴翻折后，得到l2，画出l2的图象，并求出l2的函数表达式；

（3）在（2）的条件下，点P是线段AC上点（不包括端点），过点P作x轴的平行线，分别交l2于点M，交双曲线于点N，求S△AMN的取值范围．

Answer 1

【答案】（1）；（2）y=﹣x+3；（3）≤S△AMN＜4．

【解析】

试题分析：（1）令x=1代入一次函数y=x+3后求出C的坐标，然后把C代入反比例函数解析式中即可求出k的值；

（2）设直线l2与x轴交于D，由题意知，A与D关于y轴对称，所以可以求出D的坐标，再把B点坐标代入y=ax+b即可求出直线l2的解析式；

（3）设M的纵坐标为t，由题意可得M的坐标为（3﹣t，t），N的坐标为（，t），进而得MN=+t﹣3，又可知在△ABM中，MN边上的高为t，所以可以求出S△AMN与t的关系式．

试题解析：（1）令x=1代入y=x+3，∴y=1+3=4，∴C（1，4），把C（1，4）代入中，∴k=4，∴双曲线的解析式为：；

（2）如图所示，设直线l2与x轴交于点D，由题意知：A与D关于y轴对称，∴D的坐标为（3，0），设直线l2的解析式为：y=ax+b，把D与B的坐标代入上式，得：，∴解得：，∴直线l2的解析式为：y=﹣x+3；

（3）设M（3﹣t，t），∵点P在线段AC上移动（不包括端点），∴0＜t＜4，∴PN∥x轴，∴N的纵坐标为t，把y=t代入，∴x=，∴N的坐标为（，t），∴MN=﹣（3﹣t）=+t﹣3，过点A作AE⊥PN于点E，∴AE=t，∴S△AMN=AEMN=t（+t﹣3）==．

由二次函数性质可知，当0≤t≤时，S△AMN随t的增大而减小，当＜t≤4时，S△AMN随t的增大而增大，∴当t=时，S△AMN可取得最小值为，当t=4时，S△AMN可取得最大值为4，∵0＜t＜4，∴≤S△AMN＜4．