
【题目】“冬桃”是我区某镇的一大特产,现有20箱冬桃,以每箱25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如表:
与标准质量的差值(单位:千克) |
|
|
| 0 | 0.1 | 0.25 |
箱数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20箱冬桃中,与标准质量差值为﹣0.2千克的有 筐,最重的一箱重 千克
(2)与标准重量比较,20箱冬桃总计超过多少千克?
(3)若冬桃每千克售价3元,则出售这20箱冬桃可卖多少元?
【答案】(1)4,25.25;(2)0.8千克;(3)1502.4元.
【解析】
(1)根据表格的数据分别回答即可;
(2)将20筐白菜的重量相加计算即可;
(3)将总质量乘以价格解答即可.
解:(1)25+0.25=25.25,
20筐黄桃中,与标准质量差值为﹣0.2千克的有4筐,最重的一筐重25.25千克.
故答案为:4,25.25,;
(2)1×(﹣0.3)+4×(﹣0.2)+2×(﹣0.15)+3×0+0.1×2+8×0.25
=0.8(千克).
故20筐白菜总计超过0.8千克;
(3)3×(25×20+0.8)
=3×500.8
=1502.4(元).
故出售这20筐白菜可卖1502.4元.


科目:初中数学 来源: 题型:
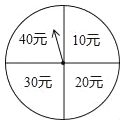
【题目】端午节期间,扬州某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图).规定:同一日内,顾客在本商场每消费满100元就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.
(1)该顾客最少可得 元购物券,最多可得 元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知∠ABC和∠ACB的平分线相交于点F,过点F作DF∥BC,交AB于点D,交AC于点E,若BD=4,DE=9,则线段CE的长为( )
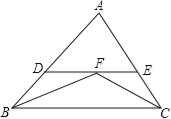
A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在坐标系中描出各点,画出三角形ABC;
(2)若三角形ABC内有一点P(![]() ,
,![]() )经平移后对应点为P1(
)经平移后对应点为P1(![]() ,
,![]() ),将三角形ABC作同样的平移得到三角形A1B1C1,画出平移后的三角形A1B1C1,并直接写出点A1,B1,C1的坐标;
),将三角形ABC作同样的平移得到三角形A1B1C1,画出平移后的三角形A1B1C1,并直接写出点A1,B1,C1的坐标;
(3)求三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE
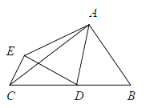
(1)求证:AD=ED
(2)连接BE,猜想△BEC的形状,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC.
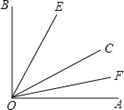
(1)若∠AOB=90°,∠AOC=30°,求∠EOF的度数;
(2)若∠AOB=![]() ,求∠EOF的度数(写出求解过程);
,求∠EOF的度数(写出求解过程);
(3)若将条件中“OE平分∠BOC,OF平分∠AOC.平分”改为“∠EOB=![]() ∠COB,∠COF=
∠COB,∠COF=![]() ∠COA”,且∠AOB=
∠COA”,且∠AOB=![]() ,求∠EOF的度数(写出求解过程).
,求∠EOF的度数(写出求解过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】典典同学学完统计知识后,随机调查了她家所在辖区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图:
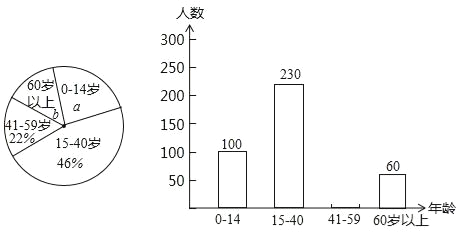
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)扇形统计图中a= ,b= ;并补全条形统计图;
(2)若该辖区共有居民3500人,请估计年龄在0~14岁的居民的人数.
(3)一天,典典知道了辖区内60岁以上的部分老人参加了市级门球比赛,比赛的老人们分成甲、乙两组,典典很想知道甲乙两组的比赛结果,王大爷告诉说,甲组与乙组的得分和为110,甲组得分不低于乙组得分的1.5倍,甲组得分最少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
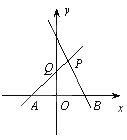
【题目】如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.
(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com