
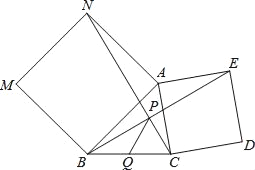
【题目】探究:如图,分别以△ABC的两边AB和AC为边向外作正方形ANMB和正方形ACDE,NC、BE交于点P.
求证:∠ANC=∠ABE.
应用:Q是线段BC的中点,若BC=6,则PQ= .
【答案】证明见解析,3
【解析】
探究:根据正方形性质得出AN=AB,AC=AE,∠NAB=∠CAE=90°,求出∠NAC=∠BAE,证出△ANC≌△ABE即可;
应用:先证明△BCP为直角三角形,然后,依据直角三角形斜边上的中线等于斜边的一半求解即可.
证明:∵四边形ANMB和ACDE是正方形,
∴AN=AB,AC=AE,∠NAB=∠CAE=90°,
∵∠NAC=∠NAB+∠BAC,∠BAE=∠BAC+∠CAE,
∴∠NAC=∠BAE,
在△ANC和△ABE中,AN=AB,∠NAC=∠BAE,AC=AE
∴△ANC≌△ABE(SAS),
∴∠ANC=∠ABE.
应用:如图所示,
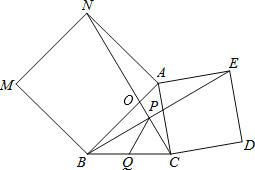
∵四边形NABM是正方形,
∴∠NAB=90°,
∴∠ANC+∠AON=90°,
∵∠BOP=∠AON,∠ANC=∠ABE,
∴∠ABP+∠BOP=90°,
∴∠BPC=∠ABP+∠BOP=90°,
∵Q为BC中点,BC=6,
∴PQ=![]() BC=3,
BC=3,


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案科目:初中数学 来源: 题型:
【题目】公园有一片长方形竹林,栽了25棵竹子,为了方便管理,每个竹子都有自己的编号,如图所示.标有2、3、5、7、10、13、17、21的竹子都在拐角处,如果![]() 处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处编号2在第1个拐角处)的竹子的编号应为( )
处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处编号2在第1个拐角处)的竹子的编号应为( )

A.10010B.10101
C.10100D.10110
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD·AB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
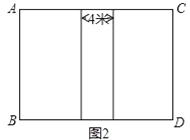
【题目】某校为学生开展拓展性课程,拟在一块长比宽多6米的长方形场地内建造由两个大棚组成的植物养殖区(如图1),要求两个大棚之间有间隔4米的路,设计方案如图2,已知每个大棚的周长为44米.
(1)求每个大棚的长和宽各是多少?
(2)现有两种大棚造价的方案,方案一是每平方米60元,超过100平方米优惠500元,方案二是每平方米70元,超过100平方米优惠总价的20%,试问选择哪种方案更优惠?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() O
O![]() 中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线
中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线![]() 和
和![]() 轴上.已知C1(1,-1),C2(
轴上.已知C1(1,-1),C2(![]() ,
, ![]() ),则点A3的坐标是________________________.
),则点A3的坐标是________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一张矩形纸片的长AD=12,宽AB=2,点E在边AD上,点F在边BC上,将四边形ABFE沿直线EF翻折后,点B落在边AD的三等分点G处,则EG的长为_______.
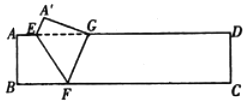
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A、B、C,完成系列问题:
(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E到A、C两点的距离相等.并在数轴上标出点E表示的数.
(3)在数轴上有一点F,满足点F到点A与点F到点C的距离和是9,则点F表示的数是 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.

(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com