
【题目】如图,已知AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD·AB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.

【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)连接OC,根据OA=OC推出∠BAC=∠OCA=∠DAC,推出OC∥AD,得出OC⊥EF,根据切线的判定推出即可;
(2)证△ADC∽△ACB,得出比例式,即可推出答案;
(3)求出等边三角形OAC,求出AC、∠AOC,在Rt△ACD中,求出AD、CD,求出梯形OCDA和扇形OCA的面积,相减即可得出答案.
试题解析:(1)证明:连接OC,
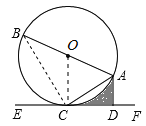
∵OA=OC,
∴∠BAC=∠OCA,
∵∠DAC=∠BAC,
∴∠OCA=∠DAC,
∴OC∥AD,
∵AD⊥EF,
∴OC⊥EF,
∵OC为半径,
∴EF是⊙O的切线.
(2)证明:连接BC,
∵AB为⊙O直径,AD⊥EF,
∴∠BCA=∠ADC=90°,
∵∠DAC=∠BAC,
∴△ACB∽△ADC,
∴![]()
∴AC2=ADAB.
(3)解:∵∠ACD=30°,∠OCD=90°,
∴∠OCA=60°,
∵OC=OA,
∴△OAC是等边三角形,
∴AC=OA=OC=2,∠AOC=60°,
∵在Rt△ACD中,AD=![]() AC=
AC=![]() ×2=1,
×2=1,
由勾股定理得:DC=![]() ,
,
∴阴影部分的面积是S=S梯形OCDA-S扇形OCA= ![]() .
.


科目:初中数学 来源: 题型:
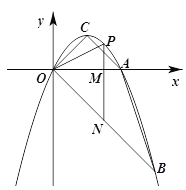
【题目】如图,抛物线y=ax2+bx经过A(2,0),B(3,-3)两点,抛物线的顶点为C,动点P在直线OB上方的抛物线上,过点P作直线PM∥y轴,交x轴于M,交OB于N,设点P的横坐标为m.
(1)求抛物线的解析式及点C的坐标;
(2)当△PON为等腰三角形时,点N的坐标为 ;当△PMO∽△COB时,点P的坐标为 ;(直接写出结果)
(3)直线PN能否将四边形ABOC分为面积比为1:2的两部分?若能,请求出m的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
(1) 求证:AG与⊙O相切;
(2)若AC=5,AB=12,BE=![]() ,求线段OE的长.
,求线段OE的长.
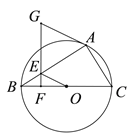
查看答案和解析>>
科目:初中数学 来源: 题型:
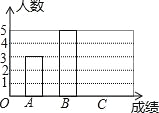
【题目】寒假结束了,为了了解九年级学生寒假体育锻炼情况,王老师调查了九年级所有学生寒假体育锻炼时间,并随即抽取10名学生进行统计,制作出如下统计图表:
编号 | 成绩 | 编号 | 成绩 |
① | B | ⑥ | A |
② | A | ⑦ | B |
③ | B | ⑧ | C |
④ | B | ⑨ | B |
⑤ | C | ⑩ | A |
根据统计图表信息解答下列问题:
(1)将条形统计图补充完整;
(2)若用扇形统计图来描述10名学生寒假体育锻炼情况,分别求A,B,C三个等级对应的扇形圆心角的度数;
(3)已知这次统计中共有60名学生寒假体育锻炼时间是A等,请你估计这次统计中B等,C等的学生各有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,已知某容器是由上下两个相同的圆锥和中间一个与圆锥同底等高的圆柱组合而成,若往此容器中注水,设注入水的体积为y,高度为x,则y关于x的函数图像大致是()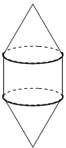
A.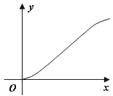
B.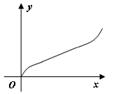
C.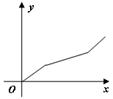
D.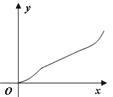
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映的过程是:小强从家去菜地浇水,又去玉米地除草,然后回家.如果菜地和玉米地的距离为a千米,小强在玉米地除草比在菜地浇水多用的时间为b分钟,则a,b的值分别为( )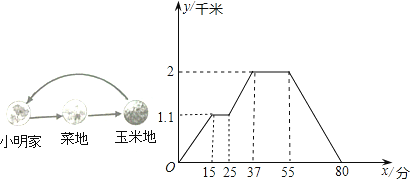
A.1.1,8
B.0.9,3
C.1.1,12
D.0.9,8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,DE 是⊙O的切线,连结OD,OE
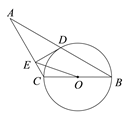
(1)求证:∠DEA=90°;
(2)若BC=4,写出求 △OEC的面积的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点A表示的数为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.![]()
(1)(1)点B表示的数为 , 点P表示的数为(用含t的式子表示);
(2)动点H从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P,H同时出发,问点P运动多少秒时追上点H?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com