
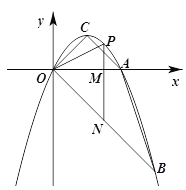
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2ЃЋbxОЙ§AЃЈ2ЃЌ0ЃЉЃЌBЃЈ3ЃЌЃ3ЃЉСНЕуЃЌХзЮяЯпЕФЖЅЕуЮЊCЃЌЖЏЕуPдкжБЯпOBЩЯЗНЕФХзЮяЯпЩЯЃЌЙ§ЕуPзїжБЯпPMЁЮyжсЃЌНЛxжсгкMЃЌНЛOBгкNЃЌЩшЕуPЕФКсзјБъЮЊmЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНМАЕуCЕФзјБъЃЛ
ЃЈ2ЃЉЕБЁїPONЮЊЕШбќШ§НЧаЮЪБЃЌЕуNЕФзјБъЮЊ ЃЛЕБЁїPMOЁзЁїCOBЪБЃЌЕуPЕФзјБъЮЊ ЃЛЃЈжБНгаДГіНсЙћЃЉ
ЃЈ3ЃЉжБЯпPNФмЗёНЋЫФБпаЮABOCЗжЮЊУцЛ§БШЮЊ1ЃК2ЕФСНВПЗжЃПШєФмЃЌЧыЧѓГіmЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉХзЮяЯпЕФНтЮіЪНЮЊyЃНЃx2ЃЋ2xЃЛCЃЈ1ЃЌ1ЃЉЃЛЃЈ2ЃЉN1ЃЈ1ЃЌЃ1ЃЉЃЌN2ЃЈ2ЃЌЃ2ЃЉЃЌN3ЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉP1ЃЈ
ЃЉP1ЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌP2ЃЈ
ЃЉЃЌP2ЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЛЃЈ3ЃЉ
ЃЉЃЛЃЈ3ЃЉ![]() Лђ
Лђ![]()
ЁОНтЮіЁПЃЈ1ЃЉБОЬташЯШИљОнХзЮяЯпy=ax2+bxЃЈaЁй0ЃЉОЙ§ЃЈ2ЃЌ0ЃЉBЃЈ3ЃЌ-3ЃЉСНЕуЃЌЗжБ№ЧѓГіaЁЂbЕФжЕЃЌдйДњШыХзЮяЯпy=ax2+bxМДПЩЧѓГіЫќЕФНтЮіЪНЃЛ
ЃЈ2ЃЉгЩЁїPONЮЊЕШбќШ§НЧаЮЕФЬѕМўЃЌвРДЮаДГіЕуNЁЂЕуPЕФзјБъЃЛ
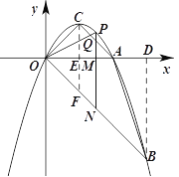
ЃЈ3ЃЉзїBDЁЭxжсгкDЃЌзїCEЁЭxжсгкEЃЌНЛOBгкFЃЌгЩШ§НЧаЮУцЛ§ЧѓГіOEЃНEFЃЌШЛКѓЗжМИжжЧщПіЕУЕНm ЕФжЕЃЎ
НтЃКЃЈ1ЃЉИљОнЬтвтЃЌЕУ![]() ЃЌНтетИіЗНГЬзщЕУ
ЃЌНтетИіЗНГЬзщЕУ![]()
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃНЃx2ЃЋ2x
ЕБxЃН![]() ЪБЃЌyЃНЃx2ЃЋ2xЃН1ЃЌЁрCЃЈ1ЃЌ1ЃЉ
ЪБЃЌyЃНЃx2ЃЋ2xЃН1ЃЌЁрCЃЈ1ЃЌ1ЃЉ
ЃЈ2ЃЉN1ЃЈ1ЃЌЃ1ЃЉЃЌN2ЃЈ2ЃЌЃ2ЃЉЃЌN3ЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉ
ЃЉ
P1ЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌP2ЃЈ
ЃЉЃЌP2ЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉ
ЃЉ
ЃЈ3ЃЉзїBDЁЭxжсгкDЃЌзїCEЁЭxжсгкEЃЌНЛOBгкF
дђBDЃНODЃН3ЃЌCEЃНOEЃН1ЃЌOCЃНAC
ЁрЁїODBЃЌЁїOCEЃЌЁїAOCОљЮЊЕШбќжБНЧШ§НЧаЮ
![]()
ЁрЁЯAOCЃНЁЯAOBЃНЁЯOACЃН45Ёу
ЁпPMЁЮyжсЃЌЁрOMЁЭPNЃЌЁЯMNOЃНЁЯAOBЃН45ЁуЃЌЁрOMЃНMNЃНmЃЌOEЃНEFЃН1
ЂйЁп![]()
ЁрЕБ0ЃМmЁм1ЪБЃЌВЛФмТњзуЬѕМў
ЂкЕБ1ЃМmЁм2ЪБЃЌЩшPNНЛACгкQЃЌдђMQЃНMAЃН2Ѓm
![]()
гЩ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
![]() ЃЌЗћКЯЬтвт
ЃЌЗћКЯЬтвт
гЩ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
![]() ЃЌЗћКЯЬтвт
ЃЌЗћКЯЬтвт
ЂлЕБ2ЃМmЃМ3ЪБЃЌзїAGЁЭxжсЃЌНЛOBгкGЃЌ
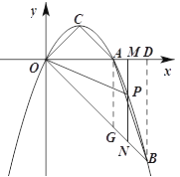
дђAGЃНOAЃН2ЃЌADЃН1
Ёр![]()
ЁрЕБ2ЃМmЃМ3ЪБЃЌВЛФмТњзуЬѕМў
Ёр![]() Лђ
Лђ![]()
ЁАЕуОІЁБДЫЬтЪєгкЖўДЮКЏЪ§злКЯЬтЃЌЩцМАСЫД§ЖЈЯЕЪ§ЗЈЧѓКЏЪ§НтЮіЪНЁЂвЛдЊвЛДЮЗНГЬЕФНтМАШ§НЧаЮЕФУцЛ§ЃЌзлКЯадНЯЧПЃЌНтД№БОЬтЕФФбЕудкЕкШ§ЮЪЃЌЙиМќЪЧИљОнЬтвтНјааЗжРрЧѓНтЃЌФбЖШНЯДѓЃЌвЛАуГіЪЧЪдЬтЕФбЙжсЬтЃЎ


 УППЮБиСЗЯЕСаД№АИ
УППЮБиСЗЯЕСаД№АИ ЧЩбЇЧЩСЗЯЕСаД№АИ
ЧЩбЇЧЩСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЪ§бЇЛюЖЏПЮЩЯЃЌаЁУїЬсГіетбљвЛИіЮЪЬтЃКЁЯB=ЁЯC=90ЁуЃЌEЪЧBCЕФжаЕуЃЌDEЦНЗжЁЯADCЃЌЁЯCED=35ЁуЃЌШчЭМЃЌдђЁЯEABЪЧЖрЩйЖШЃП 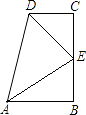
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЫЎЙћЙЋЫОвд1.5дЊ/ЧЇПЫЕФГЩБОаТНјСЫ20000ЧЇПЫИЬщйЃЌЯњЪлШЫдБЪзЯШДгЫљгаЕФИЬщйжаЫцЛњЕиГщШЁШєИЩИЬщйЃЌНјааСЫЁАИЬщйЫ№ЛЕТЪЁБЭГМЦЃЌВЂАбЛёЕУЕФЪ§ОнМЧТМдкЯТБэжаЃК
ИЬщйзмжЪСПn/ЧЇПЫ | Ы№ЛЕИЬщйжЪСПm/ЧЇПЫ | ИЬщйЫ№ЛЕЕФЦЕТЪm/n |
100 | 11.00 | 0.110 |
200 | 21.00 | 0.105 |
300 | 30.30 | |
400 | 38.84 | |
500 | 48.50 | |
600 | 61.86 | |
700 | 70.64 | |
800 | 78.48 | |
900 | 89.14 | |
1000 | 103.08 |
ЃЈ1ЃЉЧыФуЭъГЩБэИёЃЛ
ЃЈ2ЃЉШчЙћЙЋЫОЯЃЭћетаЉИЬщйФмЙЛЛёЕУЫАЧАРћШѓ10000дЊвдЩЯЃЌФЧУДдкГіЪлИЬщйЃЈвбШЅЕєЫ№ЛЕЕФИЬщйЃЉЪБЃЌДѓдМУПЧЇПЫЖЈМлЮЊЖрЩйдЊБШНЯКЯЪЪЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCКЭЁїDECжаЃЌвбжЊAB=DEЃЌВЙГфЯТСавЛзщЬѕМўЃЌШдЮоЗЈХаЖЈЁїABCЁеЁїDECЕФЪЧЃЈ ЃЉ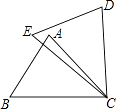
A.BC=ECЃЌЁЯB=ЁЯE
B.BC=ECЃЌAC=DC
C.ЁЯB=ЁЯEЃЌЁЯA=ЁЯD
D.BC=ECЃЌЁЯA=ЁЯD
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЮвЪаПЊеЙЕФЁАЁЎаТЛЊБЁЏжабЇЫЋгяПЮЭтдФЖСЁБЛюЖЏжаЃЌФГжабЇЮЊСЫНтАЫФъМЖ400УћбЇЩњЖСЪщЧщПіЃЌЫцЛњЕїВщСЫАЫФъМЖ50УћбЇЩњЖСЪщЕФВсЪ§ЃЎЭГМЦЪ§ОнШчЯТБэЫљЪОЃК
ВсЪ§ | 0 | 1 | 2 | 3 | 4 |
ШЫЪ§ | 2 | 10 | 15 | 17 | 6 |
ЃЈ1ЃЉЧѓет50ИібљБОЪ§ОнЕФжкЪ§КЭжаЮЛЪ§ЃЛ
ЃЈ2ЃЉИљОнбљБОЪ§ОнЃЌЙРМЦИУаЃАЫФъМЖ400УћбЇЩњдкБОДЮЛюЖЏжаЖСЪщЖргк2ВсЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§ЭМЯѓОЙ§ЃЈЉ1ЃЌ0ЃЉЃЌЃЈ3ЃЌ0ЃЉЃЌЃЈ1ЃЌЉ8ЃЉШ§ЕуЃЌЧѓДЫКЏЪ§ЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊABЪЧЁбOЕФжБОЖЃЌACЪЧЯвЃЌжБЯпEFОЙ§ЕуCЃЌADЁЭEFгкЕуDЃЌЁЯDAC=ЁЯBACЃЎ
ЃЈ1ЃЉЧѓжЄЃКEFЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЧѓжЄЃКAC2=ADЁЄABЃЛ
ЃЈ3ЃЉШєЁбOЕФАыОЖЮЊ2ЃЌЁЯACD=30ЁуЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com