
【题目】某水果公司以1.5元/千克的成本新进了20000千克柑橘,销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏率”统计,并把获得的数据记录在下表中:
柑橘总质量n/千克 | 损坏柑橘质量m/千克 | 柑橘损坏的频率m/n |
100 | 11.00 | 0.110 |
200 | 21.00 | 0.105 |
300 | 30.30 | |
400 | 38.84 | |
500 | 48.50 | |
600 | 61.86 | |
700 | 70.64 | |
800 | 78.48 | |
900 | 89.14 | |
1000 | 103.08 |
(1)请你完成表格;
(2)如果公司希望这些柑橘能够获得税前利润10000元以上,那么在出售柑橘(已去掉损坏的柑橘)时,大约每千克定价为多少元比较合适?
【答案】
(1)0.101|0.097|0.097|0.103|0.101|0.098|0.099|0.103
(2)解:由表可以看出,损坏的柑橘的频率稳定在0.1附近,即可知柑橘的损坏率为10%,则完好率为0.9,则可知20000千克柑橘中完好的质量为20000×0.9=18000千克。完好的柑橘实际成本为 ![]() =
= ![]() =
= ![]() =元/千克。
=元/千克。
设每千克柑橘的销价为x元,则应有(x- ![]() )×18000=10000,
)×18000=10000,
解得x≈2.3,
因此,出售柑橘时每千克大约定价为2.3元可获税前利润10000元以上
【解析】(1) ![]() 0.101,
0.101, ![]() =0.097,
=0.097, ![]() =0.097,
=0.097, ![]() =0.103,
=0.103, ![]() =0.101,
=0.101, ![]() =0.098,
=0.098, ![]() =0.099,
=0.099, ![]() =0.103。如下表:
=0.103。如下表:
柑橘总质量n/千克 | 损坏柑橘质量m/千克 | 柑橘损坏的频率m/n |
100 | 11.00 | 0.110 |
200 | 21.00 | 0.105 |
300 | 30.30 | 0.101 |
400 | 38.84 | 0.097 |
500 | 48.50 | 0.097 |
600 | 61.86 | 0.103 |
700 | 70.64 | 0.101 |
800 | 78.48 | 0.098 |
900 | 89.14 | 0.099 |
1000 | 103.08 | 0.103 |


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】生物科技发展公司投资2000万元,研制出一种绿色保健食品.已知该产品的成本为40元/件,试销时,售价不低于成本价,又不高于180元/件.经市场调查知,年销售量y(万件)与销售单价![]() (元/件)的关系满足下表所示的规律.
(元/件)的关系满足下表所示的规律.

(1)y与![]() 之间的函数关系式是____________,自变量
之间的函数关系式是____________,自变量![]() 的取值范围为__________;
的取值范围为__________;
(2)经测算:年销售量不低于90万件时,每件产品成本降低2元,设销售该产品年获利润为![]() (万元)(
(万元)( ![]() 年销售额一成本一投资),求出年销售量低于90万件和不低于90万件时,
年销售额一成本一投资),求出年销售量低于90万件和不低于90万件时, ![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在(2)的条件下,当销售单价定为多少时,公司销售这种产品年获利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOC=80°,OE是∠BOC的角平分线,OF是OE的反向延长线.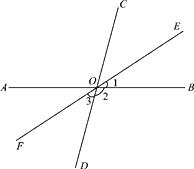
(1)求∠2、∠3的度数;
(2)说明OF平分∠AOD的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A、B两点所表示的数分别为-4、2,O为原点,点M是线段AB的中点,在线段AB上取点C,使AC = ![]() BC. 则:
BC. 则: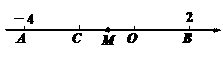
(1)求点M和点C所表示的有理数;
(2)点M是线段OC的中点吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在相同的条件下各射靶10次,每次命中的环数如下:
甲:9,7,8,9,7,6,10,10,6,8;
乙:7,8,8,9,7,8,9,8,10,6
(1)分别计算甲、乙两组数据的方差;
(2)根据计算结果比较两人的射击水平.
查看答案和解析>>
科目:初中数学 来源: 题型:
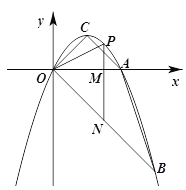
【题目】如图,抛物线y=ax2+bx经过A(2,0),B(3,-3)两点,抛物线的顶点为C,动点P在直线OB上方的抛物线上,过点P作直线PM∥y轴,交x轴于M,交OB于N,设点P的横坐标为m.
(1)求抛物线的解析式及点C的坐标;
(2)当△PON为等腰三角形时,点N的坐标为 ;当△PMO∽△COB时,点P的坐标为 ;(直接写出结果)
(3)直线PN能否将四边形ABOC分为面积比为1:2的两部分?若能,请求出m的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题:

(1)扇形统计图中m的值为 ,n的值为 ;
(2)补全条形统计图;
(3)在选择B类的学生中,甲、乙、丙三人在乒乓球项目表现突出,现决定从这三名同学中任选两名参加市里组织的乒乓球比赛,选中甲同学的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com