练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

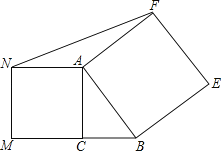
    【题目】如图，Rt△ABC，∠ACB＝90°.分别以AB，AC为边作正方形ABEF和正方形ACMN，连接FN.若AC＝4，BC＝3，则S△ANF＝______.

    【答案】6

    【解析】

    过F作FH⊥NA交NA的延长线于H，根据正方形的性质和已知条件可证明△ACB≌△AHF，由此可得FH＝BC＝3，进而可求出S△ANF.

    解：如图，过F作FH⊥AH交NA的延长线于H，

    ∵分别以AB，AC为边作正方形ABEF和正方形ACMN，

    ∴AB＝AF，∠ACB＝∠BAF＝90°，

    ∴∠CAB+∠BAH＝∠BAH+∠HAF＝90°，

    ∴∠CAB＝∠FAH，

    在△ACB和△AHF中，

    ，

    ∴△ACB≌△AHF，

    ∴BC＝HF＝3，

    ∵S△ANF＝×4×3＝6，

    故答案为：6.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】化工材料经销公司购进一种化工原料若干千克，价格为每千克30元。物价部门规定其销售单价不高于每千克60元，不低于每千克30元。经市场调查发现：日销售量y（千克）是销售单价x（元）的一次函数，且当x=60时，y=80；x=50时，y=100。在销售过程中，每天还要支付其他费用450元。

    （1）求出y与x的函数关系式，并写出自变量x的取值范围。

    （2）求该公司销售该原料日获利w（元）与销售单价x（元）之间的函数关系式。

    （3）当销售单价为多少元时，该公司日获利最大？最大获利是多少元。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB=AC，点E，F在边BC上，BE=CF，点D在AF的延长线上，AD=AC．

    （1）求证：△ABE≌△ACF；

    （2）若∠BAE=30°，则∠ADC=　 　°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】今年“五一”节，小明外出爬山，他从山脚爬到山顶的过程中，中途休息了一段时间．设他从山脚出发后所用的时间为t（分钟），所走的路程为s（米），s与t之间的函数关系如图所示，下列说法错误的是（ ）

    A．小明中途休息用了20分钟

    B．小明休息前爬山的平均速度为每分钟70米

    C．小明在上述过程中所走的路程为6600米

    D．小明休息前爬山的平均速度大于休息后爬山的平均速度

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC，交AC于点E，AC的反向延长线交⊙O于点F．

    （1）求证：DE是⊙O的切线．

    （2）若DE+EA=4，⊙O的半径为5，求CF的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

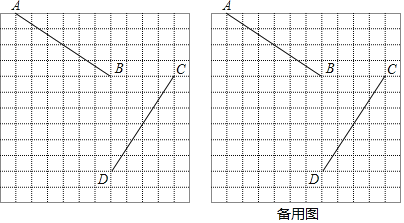
    【题目】线段AB，CD在正方形网格中的位置如图所示，将线段AB绕点O按顺时针方向旋转一定角度α，可以得到线段CD.

    (1)请在下图中画出点O；

    (2)若点A、B、C、D的坐标分别为A(﹣5，5)、B(1，1)、C(5，1)、D(1，﹣5)，则点O的坐标为_______.

    (3)α＝_____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bc+c的图象如图所示，则下列判断中错误的是（　　）

    A. 图象的对称轴是直线x=﹣1 B. 当x＞﹣1时，y随x的增大而减小

    C. 当﹣3＜x＜1时，y＜0 D. 一元二次方程ax2+bx+c=0的两个根是﹣3，1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数y=ax2+bx+c的图象经过点A（﹣1，0）、点B（3，0）、点C（4，y1），若点D（x2，y2）是抛物线上任意一点，有下列结论：

    ①二次函数y=ax2+bx+c的最小值为﹣4a；

    ②若﹣1≤x2≤4，则0≤y2≤5a；

    ③若y2＞y1，则x2＞4；

    ④一元二次方程cx2+bx+a=0的两个根为﹣1和

    其中正确结论的个数是（　　）

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】边长为，，的三角形，其内心和外心间的距离为________．

    查看答案和解析>>

    同步练习册答案