
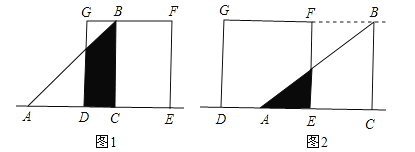
【题目】如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(阴影部分)的面积为y,
(1)求y与x之间的函数关系式;
(2)当△ABC与正方形DEFG重合部分的面积为![]() 时,求CD的长.
时,求CD的长.

【答案】(1) y=![]() x(2+2﹣x)=﹣
x(2+2﹣x)=﹣![]() x2+2x;y=
x2+2x;y=![]() (4﹣x)2;(2) CD=1或4﹣
(4﹣x)2;(2) CD=1或4﹣![]()
【解析】试题分析:(1)按照x的取值范围分为当2≤x<4时,当2≤x<4时,分段根据重合部分的图形求面积;
(2)根据(1)的分段函数,分别令y=![]() ,列方程求x的值,再根据x的取值范围进行取舍.
,列方程求x的值,再根据x的取值范围进行取舍.
试题解析:解:(1)①如图1,当0<x<2时,y=![]() x(2+2﹣x)=﹣
x(2+2﹣x)=﹣![]() x2+2x;
x2+2x;
②如图2,当2≤x<4时,y=![]() (4﹣x)2;
(4﹣x)2;
(2)①当0<x<2时,﹣![]() x2+2x=
x2+2x=![]() ,解得x1=3,x2=1,∵0<x<2,∴x=1,②当2≤x<4时,
,解得x1=3,x2=1,∵0<x<2,∴x=1,②当2≤x<4时, ![]() (4﹣x)2=
(4﹣x)2=![]() ,解得x1=4+
,解得x1=4+![]() ,x2=4﹣
,x2=4﹣![]() ,∵2≤x<4,∴x=4﹣
,∵2≤x<4,∴x=4﹣![]() ,∴CD=1或4﹣
,∴CD=1或4﹣![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. 相等的角是对顶角
B. 和为180°的两个角是邻补角
C. 两条直线被第三条直线所截,同位角相等
D. 过直线外一点,有且只有一条直线与已知直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠B=90o,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.

(1)求证:AC·AD=AB·AE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幅美丽的图案是由四个边长相等的正多边形镶嵌而成,其中的三个分别为正三角形、正四边形、正六边形,那么另外一个为( )
A. 正三角形B. 正四边形
C. 正五边形D. 正六边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com