
 如图,已知∠AOB=30°,点P在∠AOB的内部,OP=6.
如图,已知∠AOB=30°,点P在∠AOB的内部,OP=6.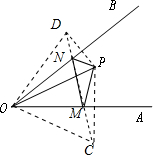


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
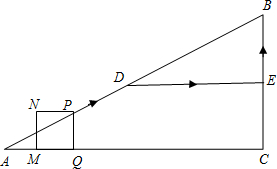 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=4cm,D、E分别为边AB、BC的中点,连结DE.点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在AD上以
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=4cm,D、E分别为边AB、BC的中点,连结DE.点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在AD上以| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
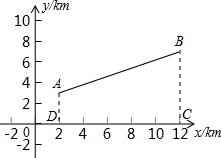 去冬今春,济宁市遭遇了200年不遇的大旱,某乡镇为了解决抗旱问题,要在某河道建一座水泵站,分别向河的同一侧张村A和李村B送水.经实地勘查后,工程人员设计图纸时,以河道上的大桥O为坐标原点,以河道所在的直线为x轴建立直角坐标系(如图).两村的坐标分别为A(2,3),B(12,7).
去冬今春,济宁市遭遇了200年不遇的大旱,某乡镇为了解决抗旱问题,要在某河道建一座水泵站,分别向河的同一侧张村A和李村B送水.经实地勘查后,工程人员设计图纸时,以河道上的大桥O为坐标原点,以河道所在的直线为x轴建立直角坐标系(如图).两村的坐标分别为A(2,3),B(12,7).查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
| 7 |
| 2.25 |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com