Question

【题目】如图1，已知点A（0，a），点B（b，0），其中a，b满足，点C（m，n）在第一象限，已知是2的立方根．

直接写出A，B，C三点的坐标；

求出△ABC的面积；

如图2，延长BC交y轴于D点，求点D的坐标；

如图3，过点C作CE∥AB交y轴于E点,求E点的坐标．

Answer 1

【答案】（1）A(0，2），B(8，0)，C(4，4)；（2）S△ABC=12；（3）D（0，8）；（4）E（0，5）.

【解析】分析：根据a，b满足，点在第一象限，已知是2的立方根．列方程求解，即可得出三点的坐标.

过点C作轴于点M，根据S△ABC=S梯形OBCM-S△AMC-S△ABO，计算即可.

设由S△ABD-S△ACD=S△ABC得，列出方程求解即可.

连接BE，设根据CE∥AB，得到列出方程求解即可.

详解：a，b满足，则：

解得：

点 在第一象限，已知是2的立方根．

则：

解得：

（2）如图，过点C作轴于点M，

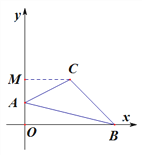
S△ABC=S梯形OBCM-S△AMC-S△ABO，

==12；

如图，设

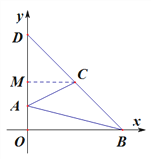
由S△ABD-S△ACD=S△ABC得，

,

解得，

∴

如图，连接BE，设

∵CE∥AB，

∴

则有，

解得，