
【题目】如图,已知抛物线y=![]() (x+2)(x﹣4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣
(x+2)(x﹣4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣![]() x+b与抛物线的另一交点为D.
x+b与抛物线的另一交点为D.

(1)若点D的横坐标为﹣5,求抛物线的函数表达式;
(2)若在第一象限内的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求k的值;
(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
【答案】(1)抛物线的函数表达式为:y=![]() (x+2)(x﹣4);
(x+2)(x﹣4);
(2)k=![]() 或k=
或k=![]() ;
;
(3)当点F坐标为(﹣2,2![]() )时,点M在整个运动过程中用时最少.
)时,点M在整个运动过程中用时最少.
【解析】
试题分析:(1)首先求出点A、B坐标,然后求出直线BD的解析式,求得点D坐标,代入抛物线解析式,求得k的值;
(2)因为点P在第一象限内的抛物线上,所以∠ABP为钝角.因此若两个三角形相似,只可能是△ABC∽△APB或△ABC∽△PAB.如答图2,按照以上两种情况进行分类讨论,分别计算;
(3)由题意,动点M运动的路径为折线AF+DF,运动时间:t=AF+![]() DF.如答图3,作辅助线,将AF+
DF.如答图3,作辅助线,将AF+![]() DF转化为AF+FG;再由垂线段最短,得到垂线段AH与直线BD的交点,即为所求的F点.
DF转化为AF+FG;再由垂线段最短,得到垂线段AH与直线BD的交点,即为所求的F点.
试题解析:(1)抛物线y=![]() (x+2)(x﹣4),
(x+2)(x﹣4),
令y=0,解得x=﹣2或x=4,
∴A(﹣2,0),B(4,0).
∵直线y=﹣![]() x+b经过点B(4,0),
x+b经过点B(4,0),
∴﹣![]() ×4+b=0,解得b=
×4+b=0,解得b=![]() ,
,
∴直线BD解析式为:y=﹣![]() x+
x+![]() .
.
当x=﹣5时,y=3![]() ,
,
∴D(﹣5,3![]() ).
).
∵点D(﹣5,3![]() )在抛物线y=
)在抛物线y=![]() (x+2)(x﹣4)上,
(x+2)(x﹣4)上,
∴![]() (﹣5+2)(﹣5﹣4)=3
(﹣5+2)(﹣5﹣4)=3![]() ,
,
∴k=![]() .
.
∴抛物线的函数表达式为:y=![]() (x+2)(x﹣4).
(x+2)(x﹣4).
(2)由抛物线解析式,令x=0,得y=﹣k,
∴C(0,﹣k),OC=k.
因为点P在第一象限内的抛物线上,所以∠ABP为钝角.
因此若两个三角形相似,只可能是△ABC∽△APB或△ABC∽△PAB.
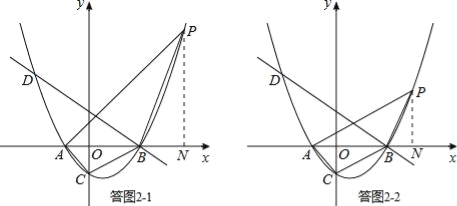
①若△ABC∽△APB,则有∠BAC=∠PAB,如答图2﹣1所示.
设P(x,y),过点P作PN⊥x轴于点N,则ON=x,PN=y.
tan∠BAC=tan∠PAB,即:![]() ,
,
∴![]() .
.
∴P(x,![]() ),代入抛物线解析式y=
),代入抛物线解析式y=![]() (x+2)(x﹣4),
(x+2)(x﹣4),
得![]() (x+2)(x﹣4)=
(x+2)(x﹣4)=![]() x+k,整理得:x2﹣6x﹣16=0,
x+k,整理得:x2﹣6x﹣16=0,
解得:x=8或x=﹣2(与点A重合,舍去),
∴P(8,5k).
∵△ABC∽△APB,
∴![]() ,即
,即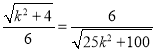 ,
,
解得:k=![]() .
.
②若△ABC∽△PAB,则有∠ABC=∠PAB,如答图2﹣2所示.
与①同理,可求得:k=![]() .
.
综上所述,k=![]() 或k=
或k=![]() .
.
(3)如答图3,由(1)知:D(﹣5,3![]() ),
),
如答图2﹣2,过点D作DN⊥x轴于点N,则DN=3![]() ,ON=5,BN=4+5=9,
,ON=5,BN=4+5=9,
∴tan∠DBA=![]() ,
,
∴∠DBA=30°.
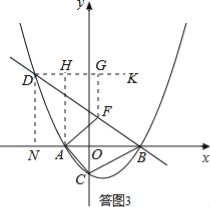
过点D作DK∥x轴,则∠KDF=∠DBA=30°.
过点F作FG⊥DK于点G,则FG=![]() DF.
DF.
由题意,动点M运动的路径为折线AF+DF,运动时间:t=AF+![]() DF,
DF,
∴t=AF+FG,即运动的时间值等于折线AF+FG的长度值.
由垂线段最短可知,折线AF+FG的长度的最小值为DK与x轴之间的垂线段.
过点A作AH⊥DK于点H,则t最小=AH,AH与直线BD的交点,即为所求之F点.
∵A点横坐标为﹣2,直线BD解析式为:y=﹣![]() x+
x+![]() ,
,
∴y=﹣![]() ×(﹣2)+
×(﹣2)+![]() =2
=2![]() ,
,
∴F(﹣2,2![]() ).
).
综上所述,当点F坐标为(﹣2,2![]() )时,点M在整个运动过程中用时最少.
)时,点M在整个运动过程中用时最少.


科目:初中数学 来源: 题型:
【题目】当今,人们对健康愈加重视,跑步锻炼成了人们的首要选择,许多与运动有关的手机APP应运而生,聪聪给自己定了目标,每天跑步![]() 公里.以目标路程为基准,超过的部分记为正,不足的部分记为负,他记下了七天的跑步路程:
公里.以目标路程为基准,超过的部分记为正,不足的部分记为负,他记下了七天的跑步路程:
日期 | 18日 | 19日 | 20日 | 21日 | 22日 | 23日 | 24日 |
路程(公里) | +1.72 | +3.20 | —1.91 | —0.96 | —1.88 | +3.30 | +0.07 |
(1)分别用含![]() 的代数式表示22日及23日的跑步路程;
的代数式表示22日及23日的跑步路程;
(2)如图所示是聪聪24日跑步路程是7.07公里,求![]() 的值;
的值;
(3)若跑步一公里消耗的热量为60千卡,请问聪聪跑步七天一共消耗了多少热量?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2018春季环境整治活动中,某社区计划对面积为1600m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用5天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y关于x的函数关系式;
(3)若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过25天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
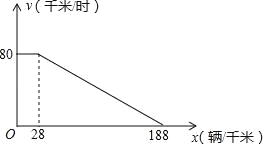
【题目】“城市发展 交通先行”,成都市今年在中心城区启动了缓堵保畅的二环路高架桥快速通道建设工程,建成后将大大提升二环路的通行能力.研究表明,某种情况下,高架桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,且当0<x≤28时,V=80;当28<x≤188时,V是x的一次函数.函数关系如图所示.
(1)求当28<x≤188时,V关于x的函数表达式;
(2)若车流速度V不低于50千米/时,求当车流密度x为多少时,车流量P(单位:辆/时)达到最大,并求出这一最大值.
(注:车流量是单位时间内通过观测点的车辆数,计算公式为:车流量=车流速度×车流密度)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位大门口有个圆形柱子,已知柱子的直径为1 m、高为5 m,为庆祝国庆节,单位想在柱子上挂一根彩带.(以下计算规定![]() =3)
=3)
(1)当彩带从A点开始绕柱子1圈后,挂在点A的正上方
的点B处,求彩带最短需要多少米?
(2)当彩带从A点开始绕柱子4圈后,挂在点A的正上方
的点B处,求彩带最短又需要多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮从家步行到公交车站台,等公交车去学校. 图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系. 下列说法错误的是

A. 他离家8km共用了30min B. 他等公交车时间为6min
C. 他步行的速度是100m/min D. 公交车的速度是350m/min
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点 O 是坐标原点,四边形 ABCO 是菱形,点 A 的坐标为(-3,4),点 C 在 x 轴的正半轴上,直线 AC 交 y 轴于点 M,AB 边交 y 轴于点 H.
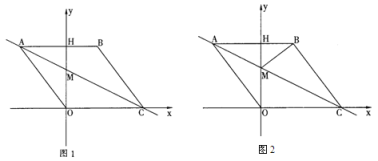
(1)求直线 AC 的解析式;
(2)连接 BM,如图 2,动点 P 从点 A 出发,沿折线 ABC 方向以 2 个单位/秒的速度向终点 C 匀速运动,设△PMB 的面积为 S(S≠0),点 P 的运动时间为t 秒,求 S 与 t 之间的函数关系式(要求写出自变量 t 的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移或轴对称或旋转对称都可以得到△OBD。
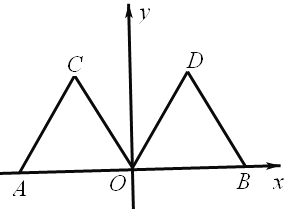
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 个单位长度;△AOC与△OBD关于直线对称,则对称轴是 ;△AOC绕原点O顺时针旋转得到△OBD,则旋转角可以是 度;
(2)连接AD,交OC于点E,求∠AEO的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com