
【题目】当今,人们对健康愈加重视,跑步锻炼成了人们的首要选择,许多与运动有关的手机APP应运而生,聪聪给自己定了目标,每天跑步![]() 公里.以目标路程为基准,超过的部分记为正,不足的部分记为负,他记下了七天的跑步路程:
公里.以目标路程为基准,超过的部分记为正,不足的部分记为负,他记下了七天的跑步路程:
日期 | 18日 | 19日 | 20日 | 21日 | 22日 | 23日 | 24日 |
路程(公里) | +1.72 | +3.20 | —1.91 | —0.96 | —1.88 | +3.30 | +0.07 |
(1)分别用含![]() 的代数式表示22日及23日的跑步路程;
的代数式表示22日及23日的跑步路程;
(2)如图所示是聪聪24日跑步路程是7.07公里,求![]() 的值;
的值;
(3)若跑步一公里消耗的热量为60千卡,请问聪聪跑步七天一共消耗了多少热量?
【答案】(1)22日的跑步路程为:(a-1.88) 公里,23日的跑步路程为:(a+3.3) 公里;(2)a=7;(3)聪聪跑步七天一共消耗了3152.4千卡热量.
【解析】
(1)根据正负数的意义表示即可;
(2)由表格可知24日跑步路程可表示为a+0.07,故a+0.07=7.07,求出a即可;
(3)将表格中数据相加得到超过或不足部分的总和,然后加上7天的总目标路程,得出的结果乘以60即可得出答案.
解:(1)∵目标路程![]() 公里为基准,超过的部分记为正,不足的部分记为负,
公里为基准,超过的部分记为正,不足的部分记为负,
∴22日的跑步路程为:(a-1.88) 公里,23日的跑步路程为:(a+3.3) 公里;
(2)由题意得:a+0.07=7.07,
∴a=7;
(3)1.72+3.20+(-1.91)+(-0.96)+ (-1.88)+3.3+0.07=3.54(公里),
(3.54+7×7)×60=3152.4(千卡),
答:聪聪跑步七天一共消耗了3152.4千卡热量.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=![]() 的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
(1)求反比例函数的解析式;
(2)通过计算说明一次函数y=mx+3﹣4m的图象一定过点C;
(3)对于一次函数y=mx+3﹣4m(m≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围,(不必写过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
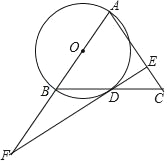
【题目】如图,在等腰△ABC中,AB=AC,以AB为直径作⊙O交边BC于点D,过点D作DE⊥AC交AC于点E,延长ED交AB的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若AB=8,AE=6,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】植树节来临之际,学校准备购进一批树苗,已知2棵甲种树苗和5棵乙种树苗共需113元;3棵甲种树苗和2棵乙种树苗共需87元.
(1)求一棵甲种树苗和一棵乙种树苗的售价各是多少元?
(2)学校准备购进这两种树苗共100棵,并且乙种树苗的数量不多于甲种树苗数量的2倍,请设计出最省钱的购买方案,并求出此时的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元初,中美洲马雅人使用的一种数字系统与其他计数方式都不相同,它采用二十进位制但只有3个符号,用点“![]() ”、划“—”、卵形“
”、划“—”、卵形“![]() ”来表示我们所使用的自然数,如自然数1-19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
”来表示我们所使用的自然数,如自然数1-19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
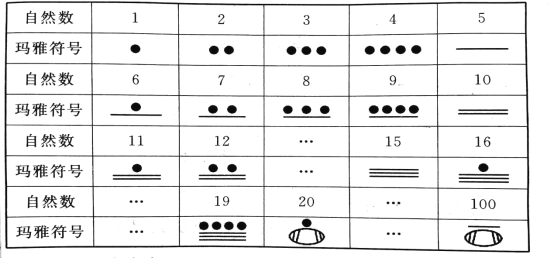
(1)玛雅符号![]() 表示的自然数是哪个数;
表示的自然数是哪个数;
(2)请你画出表示自然数280的玛雅符号.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家公司准备招聘一名英文翻译,对甲、乙和丙三名应试者进行了听、说、读、写 的英语水平测试,他们各项的成绩(百分制)如下:
应试者 | 听 | 说 | 读 | 写 |
甲 | 82 | 86 | 78 | 75 |
乙 | 73 | 80 | 85 | 82 |
丙 | 81 | 82 | 80 | 79 |
(1)如果这家公司按照这三名应试者的平均成绩(百分制)计算,从他们的成绩看,应该录取谁?
(2)如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照 3∶4∶2∶1 的权重确定,计算三名应试者的平均成绩(百分制),从他们的成绩看, 应该录取谁?
(3)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照 1∶2∶3∶4 的权重确定,计算三名应试者的平均成绩(百分制).从他们的成绩看, 应该录取谁?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为
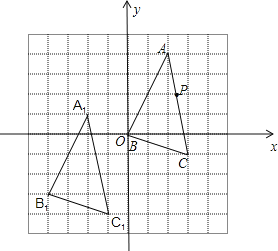
A.(1.4,-1) B.(1.5,2) C.(1.6,1) D.(2.4,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市拟购进甲乙两种大米,购进计划见下表:
品种 项目 | 数量 (单位:kg) | 进价 (单位:元/kg) | 售价的设定标准 |
甲种大米 | 600 | a | 在进价的基础上提高40% |
乙种大米 | 800 | b | 在进价的基础上提高30% |
(1)若计划购进的大米全部售出,超市可获利多少元?(用含有a,b的代数式表示结果)
(2)由于包装袋破损,两种大米混合在一起,无法分装,超市决定以散装米出售,售价为![]() 元/kg,若这批大米全部售出,超市是赚钱还是亏本,请说明理由?
元/kg,若这批大米全部售出,超市是赚钱还是亏本,请说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() (x+2)(x﹣4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣
(x+2)(x﹣4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣![]() x+b与抛物线的另一交点为D.
x+b与抛物线的另一交点为D.

(1)若点D的横坐标为﹣5,求抛物线的函数表达式;
(2)若在第一象限内的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求k的值;
(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com