
����Ŀ��̨��ij�������ꡰ��һ���ڼ俪ʼӪҵ��Ϊ�����ο�������������Ϣ��������һ���չ�˾�ɹ�һ�����������Σ����˽⣬��˾���������ͺ������Σ����±���

�����ɹ����������ι���ȥ56000Ԫ�����õ��������ÿ���1300���ο�ͬʱʹ�ã�
��1�������ɹ��˶����������Σ������������Σ�
��2�������ּƻ�����A��B�����ͺŵĿ�����20�������������˻ؾ�������֪A�Ϳ���ÿ����ͬʱװ��4�������κ�11�������Σ�B�Ϳ���ÿ����ͬʱװ��12�������κ�7�������Σ���ΰ���A��B���ֿ�����һ���Խ������������˻�����
��3����֪A�Ϳ���ÿ�����˷�Ϊ1200Ԫ��B�Ϳ���ÿ�����˷�Ϊ1050Ԫ���ڣ�2���������£���Ҫʹ�˴��˷����٣�Ӧ��ȡ���ַ�������������ٵ��˷�Ϊ����Ԫ��
���𰸡���1���ɹ���100�������Σ�200��������.
��2���������������һ���Խ������������˻��������������ţ�
����һ��A�Ϳ���15����B�Ϳ���5����
��������A�Ϳ���16����B�Ϳ���4����
��������A�Ϳ���17����B�Ϳ���3��.
��3��ʡǮ�������������A�Ϳ���15����B�Ϳ���5��������˷�Ϊ23250Ԫ
����������������1���辰���ɹ�������x����������y����Ȼ������ο������ͻ���Ǯ������������ϵ�г���������⼴�ɣ���2��������A�Ϳ���m����������B�ֿ�����20-m���������������ͺſ���װ�˵������ε�������С�����������ε������г�����ʽ�飬��⼴�ɣ��ٸ��ݳ�������������д����Ʒ�������3������ܷ���ΪWԪ���г�W�ı���ʽ���ٸ���һ�κ�����������������ٷ��ã�
�����������1���辰���ɹ�������x����������y����������ã�
![]() ���
���![]()
�ʲɹ���100�������Σ�200��������.
��2��������A�Ϳ���m����������B�ֿ�����20-m�������������
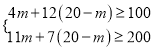 �� ��ã�15��m��17.5��
�� ��ã�15��m��17.5��
�������֪��mΪ����������mֻ��ȡ15��16��17.
���������������һ���Խ������������˻��������������ţ�
����һ��A�Ϳ���15����B�Ϳ���5����
��������A�Ϳ���16����B�Ϳ���4����
��������A�Ϳ���17����B�Ϳ���3��.
��3������ܷ���ΪWԪ����W=1200m+1050(20-m)=150m+21000��
��150��0����W��m������������֡�15��m��17.5��
�൱m=15ʱ��W����Сֵ�� ![]() =150��15+21000=23250��
=150��15+21000=23250��
����ʡǮ�������������A�Ϳ���15����B�Ϳ���5��������˷�Ϊ23250Ԫ.


 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���P�ڵ��������ڣ���P�㵽x��ľ�����3����y��ľ�����2�����P������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����֣�
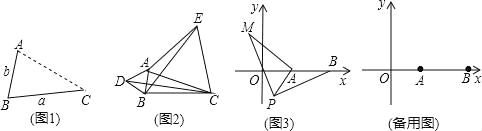
��ͼ1����AΪ�߶�BC��һ���㣬��BC=a��AB=b��
��գ�����Aλ�������� ��ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪ������ �����ú�a��b��ʽ�ӱ�ʾ��
��2��Ӧ�ã�
��AΪ�߶�BC��һ���㣬��BC=3��AB=1����ͼ2��ʾ���ֱ���AB��ACΪ�ߣ����ȱ�������ABD�͵ȱ�������ACE������CD��BE��
�����ҳ�ͼ����BE��ȵ��߶Σ���˵�����ɣ�
��ֱ��д���߶�BE�������ֵ��
��3����չ��
��ͼ3����ƽ��ֱ������ϵ�У���A������Ϊ��2��0������B������Ϊ��5��0������PΪ�߶�AB��һ���㣬��PA=2��PM=PB����BPM=90�㣬��ֱ��д���߶�AM�������ֵ����ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽��ʵ�飺�������ϵ����֡�
ʵ��Ŀ�ģ��˽�������ʱ���������ת��ʱ��������ϵ��ѧ����һԪһ�η��̽�������ϵ��й���ѧ���⣬�����ѧ��ģ˼�룮
ʵ��������е�ӣ��ֱ���һֻ
ʵ�������벽�裺
�۲���˼����
��1��ʱ��ÿ����ת��__��������ÿ����ת��__����
��2����ʱ��Ϊ8��30���������Ϊ__�������������ʱ����������ɵĽǣ�
������̽����
��1��ת�������ϵ�ʱ������룬ʹʱ��������غ���12�㴦���ٴ�ת�������ϵ�ʱ������룬��һ�㣬ʲôʱ��ʱ��������ٴ��غϣ�һ��24Сʱ�У�ʱ��������غ϶��ٴΣ���һ������ʼʱ�̺ͽ���ʱ��ʱ�������غϴ���ֻ��һ�Σ���ͬ��
��2��ת�������ϵ�ʱ������룬ʹʱ��������غ���12�㴦���ٴ�ת�������ϵ�ʱ������룬��һ�㣬ʲôʱ������ǵ�һ��Ϊ90����һ��24Сʱ�У������Ϊ90�����ٴΣ�
��չ���죺
һ��24Сʱ�У������Ϊ180��__�Σ������Ϊn����0��n��180��____�Σ���ֱ��д�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
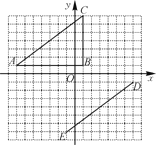
����Ŀ����ƽ��ֱ������ϵ�У���ABC�Ķ���������A(��7��1)��B(1��1)��C(1��7)���߶�DE�Ķ˵�������D(7����1)��E(��1����7)��
(1)��˵�����ƽ���߶�AC��ʹ�����߶�ED�غϣ�
(2)����ABC������ԭ��O��ʱ����ת��ʹAC�Ķ�Ӧ��ΪDE����ֱ��д����B�Ķ�Ӧ��F�����ꣻ
(3)����(2)�еġ�DEF�����͡�ABCͬʱ������ԭ��O��ʱ����ת90��.������ת���ͼ�Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ߵij��ֱ���3��7����������ε����ߵij������ǣ� ��
A. 1 B. 2 C. 8 D. 11
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ľߵ����ͬ���ĸֱʺͱ��ӣ��ֱ�ÿ֧18Ԫ������ÿ��2Ԫ�����̵��Ƴ����Żݷ���Ϊ��һ֧�ֱ����������ӣ����̵���Żݷ���Ϊ���ܼ۵ľ����Żݣ�С���빺��5֧�ֱʣ�����x����x��10��
��1���������̵깺��Ӧ���� ��Ԫ���ô���ʽ��ʾ����
��2���������̵깺��Ӧ���� ��Ԫ���ô���ʽ��ʾ����
��3����С��Ҫ��ı���Ϊ10����Ӧѡ���ļ��̵ꣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ��
��1����4a2��3a������2a2+a��1��������a��4��
��2����֪m��n��Ϊ��������2��mn��3m2����m2+5 ��mn��m2����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ��������������y=2x��ͼ���ڵ�A��m��2������y��Ľ���ΪC����x��Ľ���ΪD�� 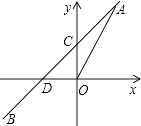
��1��m=��
��2����һ�κ���ͼ����B����2����1������һ�κ����Ľ���ʽ��
��3���ڣ�2���������£����AOD�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com