
【题目】如图,一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D. 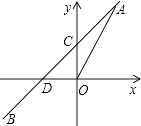
(1)m=;
(2)若一次函数图象经过点B(﹣2,﹣1),求一次函数的解析式;
(3)在(2)的条件下,求△AOD的面积.
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】台州某景区今年“五一”期间开始营业,为方便游客在园区内游玩休息,决定向一家园艺公司采购一批户外休闲椅,经了解,公司出售两种型号休闲椅,如下表:

景区采购这批休闲椅共用去56000元,购得的椅子正好可让1300名游客同时使用.
(1)求景区采购了多少条长条椅,多少条弧形椅?
(2)景区现计划租用A、B两种型号的卡车共20辆将这批椅子运回景区,已知A型卡车每辆可同时装运4条长条椅和11条弧形椅,B型卡车每辆可同时装运12条长条椅和7条弧形椅.如何安排A、B两种卡车可一次性将这批休闲椅运回来?
(3)又知A型卡车每辆的运费为1200元,B型卡车每辆的运费为1050元,在(2)的条件下,若要使此次运费最少,应采取哪种方案?并求出最少的运费为多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A. (ab3)2=a2b6 B. a2·a3=a6 C. (a+b)(a-2b)=a2-2b2 D. 5a-2a=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,连接A2B1并延长到点B2,使A2B1=B1B2 ,以A2B2为边作等边△A2B2C2,A3为等边△A2B2C2的中心,连接A3B2并延长到点B3, 使A3B2=B2B3,以A3B3为边作等边△A3B3C3,依次作下去得到等边△AnBnCn,则等边△A6B6C6的边长为_____.
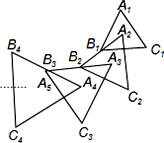
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=3ax2+2bx+c(a≠0)。
(1)若a=b=1,C=-1。求此抛物线与x轴的交点的坐标;
(2)若a=![]() ,c=b+2,其中b是整数。
,c=b+2,其中b是整数。
①直接写出抛物线的顶点坐标(用含有b的代数式表示),并写出顶点纵坐标的最大值;
②若抛物线在-2≤x≤2时,抛物线的最小值是-3,求b的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com