
【题目】已知抛物线y=3ax2+2bx+c(a≠0)。
(1)若a=b=1,C=-1。求此抛物线与x轴的交点的坐标;
(2)若a=![]() ,c=b+2,其中b是整数。
,c=b+2,其中b是整数。
①直接写出抛物线的顶点坐标(用含有b的代数式表示),并写出顶点纵坐标的最大值;
②若抛物线在-2≤x≤2时,抛物线的最小值是-3,求b的值。
【答案】(1)抛物线与x轴的交点的坐标是(-1,0),(![]() ,0)
,0)
(2)①抛物线的顶点坐标(-b,-b2+b+2),最大值是2;②b=3满足题意
【解析】分析:(1)将a、b、c的值代入,可得出抛物线解析式,从而可求解抛物线与x轴的交点坐标;(2)a=![]() ,c-b=2,则抛物线可化为y=
,c-b=2,则抛物线可化为y=![]() +2bx+b+2,其对称轴为x= -b,分x= -b<-1,x= - b>2两种情况讨论b的取值,根据最小值为-3,可得出方程,求出b的值即可.
+2bx+b+2,其对称轴为x= -b,分x= -b<-1,x= - b>2两种情况讨论b的取值,根据最小值为-3,可得出方程,求出b的值即可.
本题解析:(1)因为a=b=1,c=-1,所以抛物线解析式y=3x2+2x-1
令y=0,得3x2+2x-1=0解得x1=-1,x2=![]()
所以此时抛物线与x轴的交点的坐标是(-1,0),(![]() ,0)。
,0)。
(2)若a=![]() ,c=b+2,其中b是整数,抛物线解析式y=x2+2bx+b+2=(x+b)2-b2+b+2
,c=b+2,其中b是整数,抛物线解析式y=x2+2bx+b+2=(x+b)2-b2+b+2
①抛物线的顶点坐标(-b,-b2+b+2),所以顶点纵坐标的最大值是2.
②a=![]() ,c=b+2,则抛物线可化为y=
,c=b+2,则抛物线可化为y=![]() +2bx+b+2,其对称轴为x=b,
+2bx+b+2,其对称轴为x=b,
当x=b<2时,即b>2,则有抛物线在x=2时取最小值为3,
此时3=![]() +2×(2)b+b+2,
+2×(2)b+b+2,
解得:b=3,符合题意;
当x=b>2时,即b<2,则有抛物线在x=2时取最小值为3,
此时3=![]() +2×2b+b+2,
+2×2b+b+2,
解得:b=![]() ,不合题意,舍去,
,不合题意,舍去,
当1≤b≤2时,即2≤b≤1,则有抛物线在x=b时取最小值为3,
此时3=![]() +2×(b)b+b+2,
+2×(b)b+b+2,
化简得: ![]() b5=0,
b5=0,
解得:b=![]() (不合题意,舍去),b=
(不合题意,舍去),b=![]() ,
,
综上可得:b=3或b=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D. 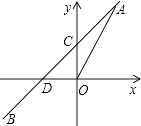
(1)m=;
(2)若一次函数图象经过点B(﹣2,﹣1),求一次函数的解析式;
(3)在(2)的条件下,求△AOD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办了“玩转数学”比赛.评委从研究报告、小组展示、答辩三个方面为每个参赛小组打分,按照研究报告占40%,小组展示占30%,答辩占30%计算各小组的成绩,各项成绩均按百分制记录.甲小组的研究报告得85分,小组展示得90分,答辩得80分,则甲小组的参赛成绩为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD。

(1)求证:DE是⊙O的切线;
(2)若tan∠ABD=2,CE=1,求⊙O的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探索新知】
己知平面上有![]() (
(![]() 为大于或等于
为大于或等于![]() 的正整数)个点
的正整数)个点![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,从第
,从第![]() 个点
个点![]() 开始沿直线滑动到另一个点,且同时满足以下三个条件:①每次滑动的距离都尽可能最大;②
开始沿直线滑动到另一个点,且同时满足以下三个条件:①每次滑动的距离都尽可能最大;②![]() 次滑动将每个点全部到达一次;③滑动
次滑动将每个点全部到达一次;③滑动![]() 次后必须回到第
次后必须回到第![]() 个点
个点![]() ,我们称此滑动为“完美运动”,且称所有点为“完美运动”的滑动点,记完成
,我们称此滑动为“完美运动”,且称所有点为“完美运动”的滑动点,记完成![]() 个点的“完美运动”的路程之和为
个点的“完美运动”的路程之和为![]() .
.
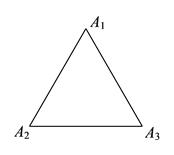
(![]() )如图
)如图![]() ,滑动点是边长为
,滑动点是边长为![]() 的等边三角形的三个顶点,此时
的等边三角形的三个顶点,此时![]() =__________.
=__________.
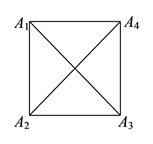
(![]() )如图
)如图![]() ,滑动点是边长为
,滑动点是边长为![]() 、对角线(线段
、对角线(线段![]() 、
、![]() )长为
)长为![]() 的正方形四个顶点,此时
的正方形四个顶点,此时![]() __________.
__________.
【深入研究】
现有![]() 个点恰好在同一直线上,相邻两点间距离都为
个点恰好在同一直线上,相邻两点间距离都为![]() .
.
(![]() )如图
)如图![]() ,当
,当![]() 时,直线上的点分别为点
时,直线上的点分别为点![]() 、
、![]() 、
、![]() .
.
![]()
为了完成“完美运动”,滑动的步骤给出如图![]() 所示的两种方法:
所示的两种方法:


方法![]() :
: ![]() , 方法
, 方法![]() :
: ![]()
①其中正确的方法为( ).
A.方法![]() B.方法
B.方法![]() C.方法
C.方法![]() 和方法
和方法![]()
②完成此“完美运动”的![]() __________.
__________.
(![]() )当
)当![]() 分别取
分别取![]() 、
、![]() 时,对应的
时,对应的![]() __________,
__________, ![]() __________.
__________.
(![]() )若直线上有
)若直线上有![]() 个点,请用含
个点,请用含![]() 的代教式表示
的代教式表示![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-6mx+9m2-9=0。
(1)求证:此方程有两个不相等的实数根;
(2)设此方程的两个根分别为x1、x2。若2x1=x2-3,求m的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一时刻,身高1.6m的小明在阳光下的影长是0.4m.同一时刻同一地点,测得某旗杆的影长是5m,则该旗杆的高度是 ( )
A.1.25mB.10mC.20mD.8m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com