
【题目】如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD。

(1)求证:DE是⊙O的切线;
(2)若tan∠ABD=2,CE=1,求⊙O的半径。
【答案】(1)证明见解析;
(2)b=3或b=![]()
【解析】分析:(1)连接OD,欲证明DE是 O的切线,只要证明OD⊥DE即可.
(2)利用相似三角形的判定和性质求出AB,利用勾股定理求出BD,进而解答即可.
本题解析:
(1)证明:连接OD。

∵OA=OD,∴∠BAD=∠ODA。∵AD平分∠BAC,∴∠BAD=∠DAC。
∴∠ODA=∠DAC。∴OD∥AE。∵DE⊥AE,∴OD⊥DE,∴DE是⊙O的切线.
(2)解:连接CD,连接DO并延长交⊙O于点F。

∵AB是⊙O直径,∴∠ADB=90°。∴∠ADB=∠E。
又∵∠BAD=∠DAC,∴△ABD∽△ADE。
∵DF是⊙O直径,∴∠FCD=90°,∴∠F=∠DAE,
∴∠F+∠FDC=90°,∠CDE+∠FDC=90°,∴∠F=∠CDE=∠DAE,
∴△DCE∽△ADE,∴∠ABD=∠DCE。根据tan∠ABD=2,∴tan∠DCE=2。
在RT△DCE中,CE=1,∴DE=2。
在RT△ADE中,同理可得AE=4,由勾股定理可知AD=2![]() 。
。
在RT△ABD中,同理可得BD=![]() ,由勾股定理可知AB=5。
,由勾股定理可知AB=5。
所以⊙O的半径为2.5。


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A. (ab3)2=a2b6 B. a2·a3=a6 C. (a+b)(a-2b)=a2-2b2 D. 5a-2a=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在4×4的正方形(每个小正方形的边长均为1)网格中,以A为顶点,其他三个顶点都在格点(网格的交点)上,且面积为2的平行四边形的共有( )个.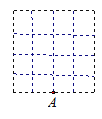
A.10
B.12
C.14
D.23
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某仓库某一天的原料进出记录如下表(运进用正数表示,运出用负数表示):
进出数量(吨) |
|
|
|
|
|
进出次数 |
|
|
|
|
|
(![]() )这天仓库的原料比原来增加了还是减少了?请说明理由.
)这天仓库的原料比原来增加了还是减少了?请说明理由.
(![]() )根据实际情况,现有两种方案.
)根据实际情况,现有两种方案.
方案一:运进每吨原料费用![]() 元,运出每吨原料费用
元,运出每吨原料费用![]() 元.
元.
方案二:不管运进还是运出费用都是每吨原料![]() 元.
元.
从节约运费的角度考虑,选用哪一种方案比较合适.
(![]() )在(
)在(![]() )的条件下,若该仓库某个月运进原料共
)的条件下,若该仓库某个月运进原料共![]() 吨,运出原料共
吨,运出原料共![]() 吨,当
吨,当![]() 、
、![]() 之间满足怎样的关系时两种方案吨运费相同.
之间满足怎样的关系时两种方案吨运费相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张长方形纸条上画一条数轴.
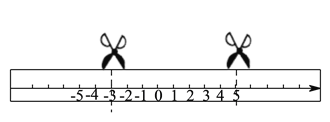
(![]() )若折叠纸条,数轴上表示
)若折叠纸条,数轴上表示![]() 的点与表示
的点与表示![]() 的点重合,则折痕与数轴的交点表示的数为__________.
的点重合,则折痕与数轴的交点表示的数为__________.
(![]() )若经过某次折叠后,该数轴伤的两个数
)若经过某次折叠后,该数轴伤的两个数![]() 和
和![]() 表示的点恰好重合,则折痕与数轴的交点表示的数为__________(用含
表示的点恰好重合,则折痕与数轴的交点表示的数为__________(用含![]() ,
, ![]() 的代数式表示).
的代数式表示).
(![]() )若将此纸条沿虚线处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折
)若将此纸条沿虚线处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折![]() 次后,再将其展开,请分别求出最左端的折痕和最右端的折痕与数轴的交点表示的数(用含
次后,再将其展开,请分别求出最左端的折痕和最右端的折痕与数轴的交点表示的数(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=3ax2+2bx+c(a≠0)。
(1)若a=b=1,C=-1。求此抛物线与x轴的交点的坐标;
(2)若a=![]() ,c=b+2,其中b是整数。
,c=b+2,其中b是整数。
①直接写出抛物线的顶点坐标(用含有b的代数式表示),并写出顶点纵坐标的最大值;
②若抛物线在-2≤x≤2时,抛物线的最小值是-3,求b的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年共享单车横空出世,更好地解决了人们“最后一公里”出行难的问题,截止到2016年底, “ofo共享单车”的投放数量是“摩拜单车”投放数量的1.6倍,覆盖城市也远超于“摩拜单车”, “ofo共享单车”注册用户量约为960万人,“摩拜单车”的注册用户量约为750万人,据统计使用一辆“ofo共享单车”的平均人数比使用一辆“摩拜单车”的平均人数少3人,假设注册这两种单车的用户都在使用共享单车,求2016年“摩拜单车”的投放数量约为多少万台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com