
 ,求m的值,并求出此时方程的两根.
,求m的值,并求出此时方程的两根.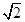 ,x2=-
,x2=-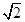 ;m=1时,x1=-2+
;m=1时,x1=-2+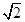 ,x2=-2-
,x2=-2-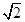 .
.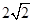 ”可以求得(x1-x2)2=(x1+x2)2-4x1x2=8,从而列出关于m的方程,通过解该方程即可求得m的值;最后将m值代入原方程并解方程.
”可以求得(x1-x2)2=(x1+x2)2-4x1x2=8,从而列出关于m的方程,通过解该方程即可求得m的值;最后将m值代入原方程并解方程.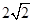
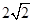 )2
)2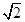 ,x2=-
,x2=-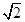
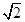 ,x2=-2-
,x2=-2-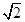


科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 %(
%( 为正整数),每箱售价提高了
为正整数),每箱售价提高了 %,成本增加了50%,其销售利润仅为去年当天利润的50%.则
%,成本增加了50%,其销售利润仅为去年当天利润的50%.则 的值为 .
的值为 .查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com