
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
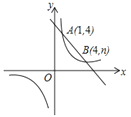
(1)求反比例函数的解析式;
(2)点![]() 是
是![]() 轴上的一动点,试确定点
轴上的一动点,试确定点![]() 的坐标,使
的坐标,使![]() 最小;
最小;
(3)直线![]() 与线段
与线段![]() 有交点,直接写出
有交点,直接写出![]() 的取值范围.
的取值范围.
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】已知点O是△ABC的外心,作正方形OCDE,下列说法:①点O是△AEB的外心;②点O是△ADC的外心;③点O是△BCE的外心;④点O是△ADB的外心.其中一定不成立的说法是( )
A.②④B.①③C.②③④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x﹣3)2+![]() (a≠0)过点C(0,4),顶点为M,与x轴交于A,B两点.如图所示以AB为直径作圆,记作⊙D.
(a≠0)过点C(0,4),顶点为M,与x轴交于A,B两点.如图所示以AB为直径作圆,记作⊙D.
(1)试判断点C与⊙D的位置关系;
(2)直线CM与⊙D相切吗?请说明理由;
(3)在抛物线上是否存在一点E,能使四边形ADEC为平行四边形.
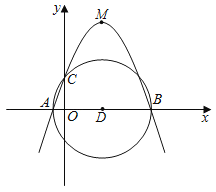
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P.
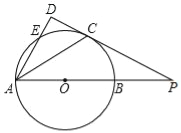
(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若tan∠P=![]() ,AD=6,求线段AE的长.
,AD=6,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机下载一个APP,缴纳一定数额的押金,就能以每小时0.5到1元的价格解锁一辆自行车任意骑行…最近的网红非“共享单车”莫属.共享单车为解决市民出行的“最后一公里”难题帮了大忙,人们在享受科技进步、共享经济带来的便利的同时,随意停放、加装私锁、大卸八块等毁坏单车的行为也层出不穷.某共享单车公司一月投入部分自行车进入市场,一月底发现损坏率不低于10%,二月初又投入1200辆进入市场,使可使用的自行车达到7500辆.
(1)一月份该公司投入市场的自行车至少有多少辆?
(2)二月份的损坏率达到20%,进入三月份,该公司新投入市场的自行车比二月份增长4a%,由于媒体的关注,毁坏共享单车的行为引起了一场国民素质的大讨论,三月份的损坏率下降![]() a%,三月底可使用的自行车达到7752辆,求a的值.
a%,三月底可使用的自行车达到7752辆,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
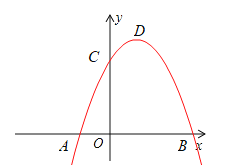
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,顶点为点
,顶点为点![]() .
.
(1)点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 ;(用含有
的坐标为 ;(用含有![]() 的代数式表示)
的代数式表示)
(2)连接![]() .
.
①若![]() 平分
平分![]() ,求二次函数的表达式;
,求二次函数的表达式;
②连接![]() ,若
,若![]() 平分
平分![]() ,求二次函数的表达式.
,求二次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
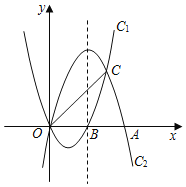
【题目】如图,抛物线C1:y=x2﹣2x与抛物线C2:y=ax2+bx开口大小相同、方向相反,它们相交于O,C两点,且分别与x轴的正半轴交于点B,点A,OA=2OB.
(1)求抛物线C2的解析式;
(2)在抛物线C2的对称轴上是否存在点P,使PA+PC的值最小?若存在,求出点P的坐标,若不存在,说明理由;
(3)M是直线OC上方抛物线C2上的一个动点,连接MO,MC,M运动到什么位置时,△MOC面积最大?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防“流感”,某学校在休息日用“药熏”消毒法对教室进行消毒.已知药物释放过程中,室内每立方米的含药量y(毫克)与时间x(时)成正比例;药物释放结束后,y与x成反比例;如图所示,根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的两个函数解析式;
(2)据测定,当药物释放结束后,每立方米的含药量降至0.25毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多长时间,学生才能进入教室?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com