
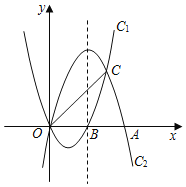
【题目】如图,抛物线C1:y=x2﹣2x与抛物线C2:y=ax2+bx开口大小相同、方向相反,它们相交于O,C两点,且分别与x轴的正半轴交于点B,点A,OA=2OB.
(1)求抛物线C2的解析式;
(2)在抛物线C2的对称轴上是否存在点P,使PA+PC的值最小?若存在,求出点P的坐标,若不存在,说明理由;
(3)M是直线OC上方抛物线C2上的一个动点,连接MO,MC,M运动到什么位置时,△MOC面积最大?并求出最大面积.
【答案】(1)y=﹣x2+4x;(2)线段OC的长度![]() ;(3)S△MOC最大值为
;(3)S△MOC最大值为![]() .
.
【解析】
(1)C1、C2:y=ax2+bx开口大小相同、方向相反,则a=-1,将点A的坐标代入C2的表达式,即可求解;
(2)点A关于C2对称轴的对称点是点O(0,0),连接OC交函数C2的对称轴与点P,此时PA+PC的值最小,即可求解;
(3)S△MOC=![]() MH×xC=
MH×xC=![]() (-x2+4x-x)= -
(-x2+4x-x)= -![]() x2+
x2+![]() x,即可求解.
x,即可求解.
(1)令:y=x2﹣2x=0,则x=0或2,即点B(2,0),
∵C1、C2:y=ax2+bx开口大小相同、方向相反,则a=﹣1,
则点A(4,0),将点A的坐标代入C2的表达式得:
0=﹣16+4b,解得:b=4,
故抛物线C2的解析式为:y=﹣x2+4x;
(2)联立C1、C2表达式并解得:x=0或3,
故点C(3,3),
连接OC交函数C2的对称轴与点P,
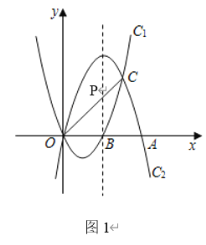
此时PA+PC的值最小为:线OC的长度![]() ;
;
设OC所在直线方程为:![]()
将点O(0,0),C(3,3)带入方程,解得k=1,
所以OC所在直线方程为:![]()
![]() 点P在函数C2的对称轴上,令x=2,带入直线方程得y=2,
点P在函数C2的对称轴上,令x=2,带入直线方程得y=2,
![]() 点P坐标为(2,2)
点P坐标为(2,2)
(3)由(2)知OC所在直线的表达式为:y=x,
过点M作y轴的平行线交OC于点H,
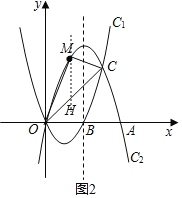
设点M(x,﹣x2+4x),则点H(x,x),则MH=﹣x2+4x﹣x
则S△MOC=S△MOH+S△MCH
=![]() MH×xC =
MH×xC = ![]() (﹣x2+4x﹣x)=
(﹣x2+4x﹣x)=![]()
∵△MOC的面积是一个关于x的二次函数,且开口向下
![]() 其顶点就是它的最大值。其对称轴为x=
其顶点就是它的最大值。其对称轴为x=![]() =
=![]() ,此时y=
,此时y=![]()
S△MOC最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是CB,AB的中点,连接CF并延长,与DA的延长线交于点M,连接DE交CF于点P,连接AP,则有下列结论:①∠BCF=∠CDE;②AP=AD:③CM=CD+DE;④S△CDM=5S四边形EPFB,其中正确的结论有( )
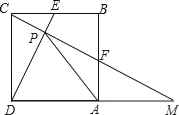
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济水平的不断提升,越来越多的人选择到电影院去观看电影,体验视觉盛宴,并且更多的人通过淘票票,猫眼等网上平台购票,快捷且享受更多优惠,电影票价格也越来越便宜.2018年从网上平台购买5张电影票的费用比在现场购买3张电影票的费用少10元,从网上平台购买4张电影票的费用和现场购买2张电影票的费用共为190元.
(1)请问2018年在网上平台购票和现场购票的每张电影票的价格各为多少元?
(2)2019年“元旦”当天,南坪上海城的“华谊兄弟影院”按照2018年在网上平台购票和现场购票的电影票的价格进行销售,当天网上和现场售出电影票总票数为600张.“元旦”假期刚过,观影人数出现下降,于是该影院决定将1月2日的现场购票的价格下调,网上购票价格保持不变,结果发现现场购票每张电影票的价格每降价0.5元,则当天总票数比“元旦”当天总票数增加4张,经统计,1月2日的总票数中有![]() 通过网上平台售出,其余均由电影院现场售出,且当天票房总收益为19800元,请问该电影院在1月2日当天现场购票每张电影票的价格下调了多少元?
通过网上平台售出,其余均由电影院现场售出,且当天票房总收益为19800元,请问该电影院在1月2日当天现场购票每张电影票的价格下调了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(-3,﹣2)两点.
的图象交于A(2,m),B(-3,﹣2)两点.
(1)求m的值;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点, 且y1>y2,求实数p的取值范围.
图象上的两点, 且y1>y2,求实数p的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解本校九年级学生期末数学考试情况,在九年级随机抽取了一部分学生 的期末数学成绩为样本,分为 A(90~100 分);B(80~89 分);C(60~79 分);D(0~59 分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下 问题.
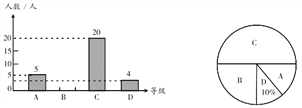
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生 1200 人,若分数为 80 分(含 80 分)以上为优秀,请估 计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形A0B0C0A1的边长为1,正方形A1B1C1A2的边长为2,正方形A2B2C2A3的边长为4,正方形A3B3C3A4的边长为8……依此规律继续作正方形AnBnnAn+1,且点A0,A1,A2,A3,…,An+1在同一条直线上,连接A0C1交A1B1于点D1,连接A1C2交A2B2于点D2,连接A2C3交A3B3于点D3……记四边形A0B0C0D1的面积为S1,四边形A1B1C1D2的面积为S2,四边形A2B2C2D3的面积为S3……四边形An﹣1Bn﹣1Cn﹣1Dn的面积为Sn,则S2019=_____.
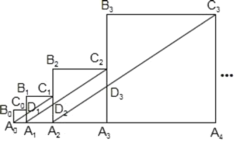
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮分别从甲地和乙地同时出发,沿同一条路相向而行,小明开始跑步,中途改为步行,到达乙地恰好用![]() 小亮骑自行车以
小亮骑自行车以![]() 的速度直接到甲地,两人离甲地的路程
的速度直接到甲地,两人离甲地的路程![]() 与各自离开出发地的时间
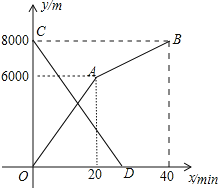
与各自离开出发地的时间![]() 之间的函数图象如图所示,
之间的函数图象如图所示,
![]() 甲、乙两地之间的路程为______m,小明步行的速度为______
甲、乙两地之间的路程为______m,小明步行的速度为______![]() ;
;
![]() 求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
![]() 求两人相遇的时间.
求两人相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
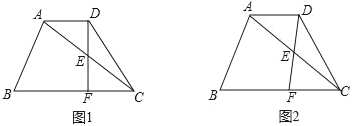
【题目】已知在梯形ABCD中,AD∥BC,AC=BC=10,cos∠ACB=![]() ,点E在对角线AC上(不与点A、C重合),∠EDC=∠ACB,DE的延长线与射线CB交于点F,设AD的长为x.
,点E在对角线AC上(不与点A、C重合),∠EDC=∠ACB,DE的延长线与射线CB交于点F,设AD的长为x.
(1)如图1,当DF⊥BC时,求AD的长;
(2)设EC=y,求y关于x的函数解析式,并直接写出定义域;
(3)当△DFC是等腰三角形时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com