
【题目】小明和小亮分别从甲地和乙地同时出发,沿同一条路相向而行,小明开始跑步,中途改为步行,到达乙地恰好用![]() 小亮骑自行车以
小亮骑自行车以![]() 的速度直接到甲地,两人离甲地的路程
的速度直接到甲地,两人离甲地的路程![]() 与各自离开出发地的时间
与各自离开出发地的时间![]() 之间的函数图象如图所示,
之间的函数图象如图所示,
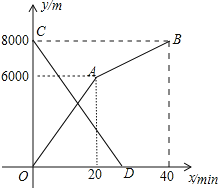
![]() 甲、乙两地之间的路程为______m,小明步行的速度为______
甲、乙两地之间的路程为______m,小明步行的速度为______![]() ;
;
![]() 求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
![]() 求两人相遇的时间.
求两人相遇的时间.
科目:初中数学 来源: 题型:
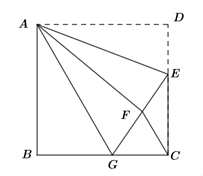
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
①△ABG≌△AFG;②BG=GC;③AG∥CF;④![]() .
.
其中正确结论的个数是( )
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线y=x+b与双曲线y=![]() (x<0)交于点A(﹣1,﹣5),并分别与x轴、y轴交于点C、B.
(x<0)交于点A(﹣1,﹣5),并分别与x轴、y轴交于点C、B.
(1)求出b、m的值;
(2)点D在x轴的正半轴上,若以点D、C、B组成的三角形与△OAB相似,试求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:如果存在常数![]() ,对于任意的函数值
,对于任意的函数值![]() ,都满足
,都满足![]() ≤
≤![]() ,那么称这个函数是有上界函数;在所有满足条件的
,那么称这个函数是有上界函数;在所有满足条件的![]() 中,其最小值称为这个函数的上确界.例如,函数
中,其最小值称为这个函数的上确界.例如,函数![]() ,
, ![]() ≤2,因此是有上界函数,其上确界是2.如果函数
≤2,因此是有上界函数,其上确界是2.如果函数![]() (
(![]() ≤x≤
≤x≤![]() ,
, ![]() <
<![]() )的上确界是
)的上确界是![]() ,且这个函数的最小值不超过2
,且这个函数的最小值不超过2![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() ≤
≤![]() B.
B. ![]() C.
C. ![]() ≤
≤![]() D.
D. ![]() ≤
≤![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学分别进行6次射击训练,训练成绩(单位:环)如下表 对他们的训练成绩作如下分析,其中说法正确的是( )
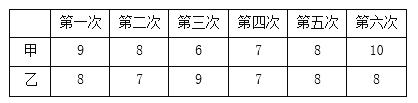
A. 他们训练成绩的平均数相同
B. 他们训练成绩的中位数不同
C. 他们训练成绩的方差不同
D. 他们训练成绩的众数不同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
“三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆、外接圆的圆心叫做三角形的外心,这个三角形叫做这个圆的内接三角形。”(苏科版《数学》九上 2.3确定圆的条件)
问题初探:
(1)三角形的外心到三角形的_____________距离相等
(2)若点O是△ABC的外心,试探索∠BOC与∠BAC之间的数量关系。
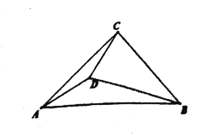
(3)如图,在Rt△ABC中,∠ACB=90°,AC=BC。将线段BC绕点B逆时针旋转30°到BD,连接AD、CD。用直尺和圆规在图中作出△BCD的外心O,并求∠ADB的度数。(保留作图痕迹,不写作法。)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com