
【题目】如图,已知△EFG≌△NMH,∠F与∠M是对应角.
(1)写出相等的线段与角.
(2)若EF=2.1cm,FH=1.1cm,HM=3.3cm,求MN和HG的长度.

【答案】(1)EF=NM,EG=NH,FG=MH,∠F=∠M, ∠E=∠N, ∠EGF=∠NHM(2)MN=2.1cm,HG=2.2cm.
【解析】试题分析:(1)因为△EFG≌△NMH,故有全等三角形的对应边和对应角相等. (2)因为△EFG≌△NMH,故EF=NM,![]() ,即可求出各自的长度.
,即可求出各自的长度.
试题解析:(1)![]() △EFG≌△NMH,∠F与∠M是对应角
△EFG≌△NMH,∠F与∠M是对应角![]() 在△EFG和△NMH中,有EF=NM,EG=NH,FG=MH
在△EFG和△NMH中,有EF=NM,EG=NH,FG=MH
∠F=∠M, ∠E=∠N, ∠EGF=∠NHM ;(2)∵由(1)可知,EF=NM,EF=2.1cm ∴MN="2.1" 又![]() MH=FG=3.3 FH=1.1 ∴
MH=FG=3.3 FH=1.1 ∴![]() =3.3-1.1=2.2cm.
=3.3-1.1=2.2cm.
考点:全等三角形的性质.


科目:初中数学 来源: 题型:
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O ![]() C
C ![]() B
B ![]() A运动,点P的运动时间为t秒.
A运动,点P的运动时间为t秒.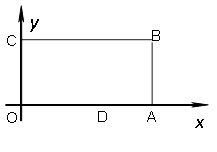
(1)当t=5时, P点坐标为( , )
(2)当t>4时,OP+PD有最小值吗?如果有,请算出该最小值,如果没有,请说明理由。
(3)当t为何值时,△ODP是腰长为5的等腰三角形?(直接写出t的值)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用总长为60cm的篱笆围成矩形场地.
(Ⅰ)根据题意,填写下表:

(Ⅱ)设矩形一边长为lm,矩形面积为Sm2,当l是多少时,矩形场地的面积S最大?并求出矩形场地的最大面积;
(Ⅱ)当矩形的长为 m,宽为 m时,矩形场地的面积为216m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从一副扑克牌中任意抽取1张.
①这张牌是“A”;
②这张牌是“红桃”;
③这张牌是“大王”;
④这张牌是“红色的”.
将这些事件按发生的可能性从小到大顺序排列 . (填序号,用“<”连接)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com