
 如图,与∠2互为同旁内角的是∠1,∠3;与∠3互为同位角的是∠4,∠5;∠6与∠9是内错角,它们是直线AC与DE被直线BE所截得的;∠3与∠5是直线AC与直线BC被直线BE所截得的;与∠1是同位角的有∠7,∠8,在标有数字的九个角中,大小一定相等的角有∠2=∠6,∠5=∠7.
如图,与∠2互为同旁内角的是∠1,∠3;与∠3互为同位角的是∠4,∠5;∠6与∠9是内错角,它们是直线AC与DE被直线BE所截得的;∠3与∠5是直线AC与直线BC被直线BE所截得的;与∠1是同位角的有∠7,∠8,在标有数字的九个角中,大小一定相等的角有∠2=∠6,∠5=∠7. 分析 根据同位角,内错角和同旁内角的定义进行判断即可,三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.
解答  解:由图可得,∠1,∠3与∠2互为同旁内角;
解:由图可得,∠1,∠3与∠2互为同旁内角;
∠4,∠5与∠3互为同位角;
∠6与∠9是内错角,它们是直线AC与DE被直线BE所截得的;
∠3与∠5是直线AC与直线BC被直线BE所截得的同位角;
∠7,∠8与∠1是同位角;
根据对顶角相等可得,在标有数字的九个角中,大小一定相等的角有∠2=∠6,∠5=∠7.
故答案为:∠1,∠3;∠4,∠5;内错角,AC,DE,BE;AC,BC,BE;∠7,∠8;∠2=∠6,∠5=∠7.
点评 本题主要考查了同位角,内错角和同旁内角的定义以及对顶角的性质,在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )| A. | ($\frac{2}{3}$,3),(-$\frac{1}{2}$,4) | B. | ($\frac{7}{4}$,$\frac{7}{2}$),($-\frac{1}{2}$,4) | C. | ($\frac{2}{3}$,3),($-\frac{2}{3}$,4) | D. | ($\frac{7}{4}$,$\frac{7}{2}$),($-\frac{2}{3}$,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9x+1-10x+1=1 | B. | 9x+3-10x-1=1 | C. | 9x+3-10x-1=12 | D. | 9x+3-10x+1=12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
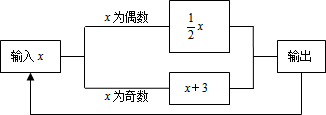 有一个程序机(如图),若输入4,则输出值是2,记作第一次操作;将2再次输入,则输出值是1,记作第二次操作…,则第2016次操作输出的数是4.
有一个程序机(如图),若输入4,则输出值是2,记作第一次操作;将2再次输入,则输出值是1,记作第二次操作…,则第2016次操作输出的数是4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com