
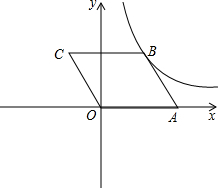
 (2012•长春)如图,在平面直角坐标系中,?OABC的顶点A、C的坐标分别为A(2,0)、C(-1,2),反比例函数y=
(2012•长春)如图,在平面直角坐标系中,?OABC的顶点A、C的坐标分别为A(2,0)、C(-1,2),反比例函数y=| k |
| x |
| k |
| x |
| 2 |
| x |
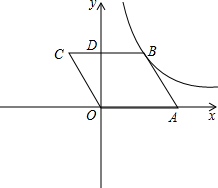 解:(1)∵四边形OABC是平行四边形,
解:(1)∵四边形OABC是平行四边形,| k |
| x |
| 2 |
| x |
| 2 |
| x |


科目:初中数学 来源: 题型:
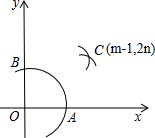 (2012•长春)如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于
(2012•长春)如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•长春)如图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查,结果为(单位:人):30,31,27,26,31.这组数据的中位数是( )
(2012•长春)如图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查,结果为(单位:人):30,31,27,26,31.这组数据的中位数是( )查看答案和解析>>
科目:初中数学 来源: 题型:
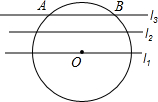 (2012•长春)如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为4,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=12,求⊙O的半径.
(2012•长春)如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为4,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=12,求⊙O的半径.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com