练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
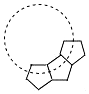
    17．如图，用若干个全等的正五边形可以拼成一个环状，如图是前3个正五边形的拼接情况，要完全拼成一个圆环还需要的正五边形个数是7．

    分析 设要完全拼成一个圆环需要的正五边形为n个，则围成的多边形为正n边形，利用正五边形的内角计算出正n边的每个内角的度数，然后根据内角和定理得到（n-2）•180°=（360°-2×108°）n，再解方程求出x即可．

    解答 解：设要完全拼成一个圆环需要的正五边形为n个，
    所以（n-2）•180°=（360°-2×108°）n，解得n=10，
    所以要完全拼成一个圆环还需要的正五边形的个数为7．
    故答案为7．

    点评 本题考查了多边形的内角与外角：多边形内角和定理：（n-2）•180 （n≥3）且n为整数）；外角和为360°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．如图1，直线y=-2x+4交x轴、y轴于A、B两点，交双曲线y=$\frac{k}{x}$（x＜0）于C点，△AOC的面积为6．
    （1）求双曲线的解析式．
    （2）如图2，D为双曲线y=$\frac{k}{x}$（x＜0）上一点，连结CD，将线段CD绕点D顺时针旋转90°得线段DE，点E恰好落在x轴上，求点E的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．如图，∠C=90°，AC=12，CB=5，AM=AC，BN=BC，则MN的长是（　　）
    A．2B．2.6C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

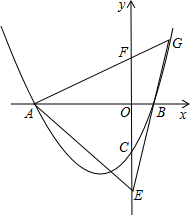    5．已知抛物线y=$\frac{1}{2}{x}^{2}+2mx-4m-2$（m≥0）与x轴交于A、B两点，A点在B点的左边．与y轴交于点C．
    （1）当AB=6时，求点C的坐标；
    （2）抛物线上有两点M（-1，a）、N（4，b），若△AMN的面积为17.5，求m的值；
    （3）在抛物线第一象限上有一点G，连接AG、GB并延长分别交y轴于F、E．若∠AFO=∠EBO，求证：点G总在一条定直线上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

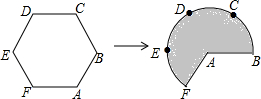    12．如图，将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心，AB为半径的扇形（忽略铁丝的粗细）．则所得扇形AFB（阴影部分）的面积为（　　）
    A．6πB．18C．18πD．20

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．当a，b互为相反数时，代数式a2+ab-4的值为（　　）
    A．4B．0C．-3D．-4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知$\sqrt{16}$的算术平方根为a，-$\sqrt{10}$的整数部分为b，则（-2a-b）2015=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

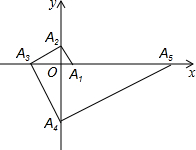    6．如图，点A1的坐标为（1，0），A2在y轴的正半轴上，且∠A1A2O=30°，过点A2作A2A3⊥A1A2，垂足为A2，交x轴于点A3，过点A3作A3A4⊥A2A3，垂足为A3，交y轴于点A4；过点A4作A4A5⊥A3A4，垂足为A4，交x轴于点A5；过点A5作A5A6⊥A4A5，垂足为A5，交y轴于点A6；…按此规律进行下去，则点A2017的横坐标为31008．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

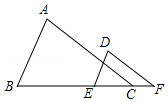    7．如图，已知点B、E、C、F在同一条直线上，∠A=∠D，要使△ABC∽△DEF，还需添加一个条件，你添加的条件是∠B=∠DEC．（只需写一个条件，不添加辅助线和字母）

    查看答案和解析>>

    同步练习册答案