
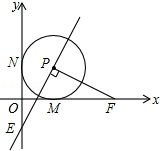
 已知在平面直角坐标系xOy中,O是坐标原点,以 P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0),作点F关于点M的对称点F′,经过M、E和F′三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似,则t的值为$\sqrt{2}$,$\frac{1+\sqrt{17}}{4}$,2±$\sqrt{2}$,.
已知在平面直角坐标系xOy中,O是坐标原点,以 P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0),作点F关于点M的对称点F′,经过M、E和F′三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似,则t的值为$\sqrt{2}$,$\frac{1+\sqrt{17}}{4}$,2±$\sqrt{2}$,. 分析 如图1当1<t<2时,由F(1+t,0),F和F′关于点M对称,得到F′(1-t,0)由经过M、E和F′三点的抛物线的对称轴交x轴于点Q,得到Q(1-$\frac{1}{2}$t),求出OQ=1-$\frac{1}{2}$t,
因为⊙P与x轴,y轴分别相切于点M和点N,求得PM⊥MF,PN⊥ON且PM=PN,所以∠PMF=∠PNE=90°且∠NPM=90°,证得△PMF≌△PNE(ASA),得到NE=MF=t,OE=t-1
当△OEQ∽△MPF时,由$\frac{OE}{MP}$=$\frac{OQ}{MF}$,求得t=$\frac{1+\sqrt{17}}{4}$,当△OEQ∽△MFP时,得到$\frac{OE}{MF}$=$\frac{OQ}{MP}$,求得t=$\sqrt{2}$;
如图2,当t>2时,由F(1+t,0),F和F′关于点M对称,得到F′(1-t,0)由经过M、E和F′三点的抛物线的对称轴交x轴于点Q,得到Q(1-$\frac{1}{2}$t,0)
求得OQ=$\frac{1}{2}$t-1,由①得△PMF≌△PNE,得到NE=MF=t,OE=t-1当△OEQ∽△MPF得到$\frac{OE}{MP}$=$\frac{OQ}{MF}$,$\frac{t-1}{1}$=$\frac{\frac{1}{2}t}{t}$,无解,
当△OEQ∽△MFP时,得到$\frac{OE}{MF}$=$\frac{OQ}{MP}$,解得t=2±$\sqrt{2}$,
所以当t=$\frac{1+\sqrt{17}}{4}$,t=$\sqrt{2}$,t=2±$\sqrt{2}$时,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似.
解答 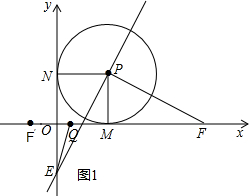 解:①如图1当1<t<2时,
解:①如图1当1<t<2时,
∵F(1+t,0),F和F′关于点M对称,
∴F′(1-t,0)
∵经过M、E和F′三点的抛物线的对称轴交x轴于点Q,
∴Q(1-$\frac{1}{2}$t,0)
∴OQ=1-$\frac{1}{2}$t,
∵⊙P与x轴,y轴分别相切于点M和点N,
∴PM⊥MF,PN⊥ON且PM=PN,
∴∠PMF=∠PNE=90°且∠NPM=90°,
∵PE⊥PF,
∠NPE=∠MPF=90°-∠MPE,
在△PMF和△PNE中,
$\left\{\begin{array}{l}{∠NPE=∠MPF}\\{PN=PM}\\{∠PNE=∠PMF}\end{array}\right.$,
∴△PMF≌△PNE(ASA),
∴NE=MF=t,
∴OE=t-1
当△OEQ∽△MPF时,
∴$\frac{OE}{MP}$=$\frac{OQ}{MF}$,∴$\frac{t-1}{1}$=$\frac{1-\frac{1}{2}t}{t}$,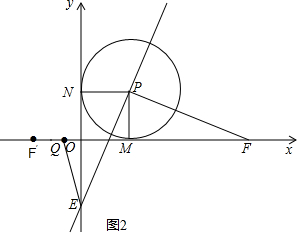
∴t=$\frac{1+\sqrt{17}}{4}$,
当△OEQ∽△MFP时,
∴$\frac{OE}{MF}$=$\frac{OQ}{MP}$,
∴$\frac{t-1}{t}$=$\frac{1-\frac{1}{2}t}{1}$,
∴t=$\sqrt{2}$;
②如图2,当t>2时,
∵F(1+t,0),F和F′关于点M对称,
∴F′(1-t,0)
∵经过M、E和F′三点的抛物线的对称轴交x轴于点Q,
∴Q(1-$\frac{1}{2}$t,0)
∴OQ=$\frac{1}{2}$t-1,
由①得△PMF≌△PNE
∴NE=MF=t,
∴OE=t-1
当△OEQ∽△MPF
∴$\frac{OE}{MP}$=$\frac{OQ}{MF}$,
∴$\frac{t-1}{1}$=$\frac{\frac{1}{2}t}{t}$,无解,
当△OEQ∽△MFP时,
∴$\frac{OE}{MF}$=$\frac{OQ}{MP}$,
∴$\frac{t-1}{t}$=$\frac{\frac{1}{2}t-1}{1}$,
解得,t=2±$\sqrt{2}$,
所以当t=$\frac{1+\sqrt{17}}{4}$,t=$\sqrt{2}$,t=2±$\sqrt{2}$时,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似.
故答案为:t=$\frac{1+\sqrt{17}}{4}$,t=$\sqrt{2}$,t=2±$\sqrt{2}$.
点评 本题主要考查了三角形相似的判定和性质,三角形全等的判定和性质,动点问题,切线的性质,抛物线的对称轴等知识点.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 可以是x=-0.2,不可以是 x=0.2 | |
| B. | 可以是x=0.2,不可以是 x=-0.2 | |
| C. | 可以是x=-0.2,也可以是 x=0.2 | |
| D. | 既不可以是x=-0.2,也不可以是 x=0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
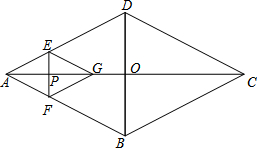 菱形ABCD的对角线AC,BD相交于点O,AC=16,BD=12,动点P在线段AC上从点A向点C以4个单位/秒的速度运动,过点P作EF⊥AC,交菱形ABCD的边于点E、F,在直线AC上有一点G,使△AEF与△GEF关于EF对称.设菱形ABCD被四边形AEGF盖住部分的面积为S1,未被盖住部分的面积为S2,点P运动时间为x秒.
菱形ABCD的对角线AC,BD相交于点O,AC=16,BD=12,动点P在线段AC上从点A向点C以4个单位/秒的速度运动,过点P作EF⊥AC,交菱形ABCD的边于点E、F,在直线AC上有一点G,使△AEF与△GEF关于EF对称.设菱形ABCD被四边形AEGF盖住部分的面积为S1,未被盖住部分的面积为S2,点P运动时间为x秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
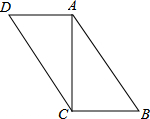 如图所示,在四边形ABCD中,已知AC⊥AD,AC=8,AD=x-10,CD=x-6,AB=10,BC=22-x.求证:四边形ABCD是平行四边形.
如图所示,在四边形ABCD中,已知AC⊥AD,AC=8,AD=x-10,CD=x-6,AB=10,BC=22-x.求证:四边形ABCD是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com