
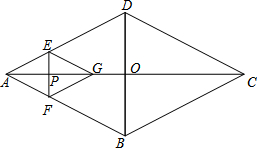
 菱形ABCD的对角线AC,BD相交于点O,AC=16,BD=12,动点P在线段AC上从点A向点C以4个单位/秒的速度运动,过点P作EF⊥AC,交菱形ABCD的边于点E、F,在直线AC上有一点G,使△AEF与△GEF关于EF对称.设菱形ABCD被四边形AEGF盖住部分的面积为S1,未被盖住部分的面积为S2,点P运动时间为x秒.
菱形ABCD的对角线AC,BD相交于点O,AC=16,BD=12,动点P在线段AC上从点A向点C以4个单位/秒的速度运动,过点P作EF⊥AC,交菱形ABCD的边于点E、F,在直线AC上有一点G,使△AEF与△GEF关于EF对称.设菱形ABCD被四边形AEGF盖住部分的面积为S1,未被盖住部分的面积为S2,点P运动时间为x秒.分析 (1)首先证得EF∥BD,证得△AEF∽△ADB,求得EF,进一步得出AP,分点P从点A到点O,从点O到点C两种情况,利用菱形的面积计算方法求得S1,S2;
(2)由(1)中的两个面积建立方程求得x的数值即可.
解答 解:(1)由题得,EF⊥AC,BD⊥AC,
∴EF∥BD
∴△AEF∽△ADB
∴$\frac{AP}{AO}=\frac{EF}{BD}$
∴EF=6x,
又∵AP=PG=4x
∴当0<x≤2时,
${S_1}=24{x^2}$,${S_2}=96-24{x^2}$,
当2<x<4时,EF=24-6x,
∴${S_1}=192-48{x^{\;}}$,S2=48x-96.
(2)当0<x≤2时,
24x2=96-24x2,
解得:x=$\sqrt{2}$;
当2<x<4时,
192-48x=48x-96,
解得:x=3.
点评 此题考查菱形的性质,相似三角形的判定与性质,掌握菱形的对角线互相垂直平分,且乘积的一半是菱形的面积是解决问题的关键.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
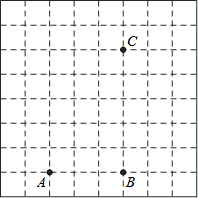 根据要求画图或作答.如图所示,已知点A、B、C是网格纸上的三个格点.
根据要求画图或作答.如图所示,已知点A、B、C是网格纸上的三个格点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一组数据1,5,3,4,6,5的中位数是5 | |
| B. | 三角形的外心是它三边垂直平分线的交点 | |
| C. | 等腰三角形是中心对称图形 | |
| D. | 六个角为120度的六边形是正六边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-2<y-2 | B. | x+2<y+2 | C. | $\frac{x}{2}$<$\frac{y}{2}$ | D. | -2x<-2y |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
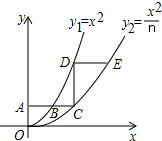 如图,平行于x轴的直线AC分别交函数y1=x2(x≥0)与y2=$\frac{{x}^{2}}{n}$(x≥0)的图象于B、C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,当n=2时,$\frac{DE}{AB}$的值为2-$\sqrt{2}$;当n=k时,$\frac{DE}{AB}$的值为k-$\sqrt{k}$.
如图,平行于x轴的直线AC分别交函数y1=x2(x≥0)与y2=$\frac{{x}^{2}}{n}$(x≥0)的图象于B、C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,当n=2时,$\frac{DE}{AB}$的值为2-$\sqrt{2}$;当n=k时,$\frac{DE}{AB}$的值为k-$\sqrt{k}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
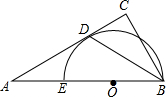 如图,在△ABC中,∠C=90°,BD平分∠ABC,E是AB上的一点,以BE为直径的⊙O过点D.
如图,在△ABC中,∠C=90°,BD平分∠ABC,E是AB上的一点,以BE为直径的⊙O过点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
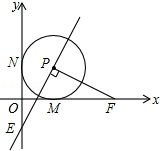 已知在平面直角坐标系xOy中,O是坐标原点,以 P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0),作点F关于点M的对称点F′,经过M、E和F′三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似,则t的值为$\sqrt{2}$,$\frac{1+\sqrt{17}}{4}$,2±$\sqrt{2}$,.
已知在平面直角坐标系xOy中,O是坐标原点,以 P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0),作点F关于点M的对称点F′,经过M、E和F′三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似,则t的值为$\sqrt{2}$,$\frac{1+\sqrt{17}}{4}$,2±$\sqrt{2}$,.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com