Question

【题目】类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．

（1）概念理解：
如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”．请写出你添加的一个条件．
（2）问题探究：
①小红猜想：对角线互相平分的“等邻边四边形”是菱形，她的猜想正确吗？请说明理由．
②如图2，小红画了一个Rt△ABC，其中∠ABC=90°，AB=2，BC=1，并将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′，连结AA′，BC′，小红要使平移后的四边形ABC′A′是“等邻边四边形”，应平移多少距离（即线段BB′的长）？
（3）拓展应用：
如图3，“等邻边四边形”ABCD中，AB=AD，∠BAD+∠BCD=90°，AC，BD为对角线，AC= AB，试探究BC，CD，BD的数量关系．

Answer 1

【答案】
（1）

解：AB=BC或BC=CD或CD=AD或AD=AB（任写一个即可）

（2）

解：①正确，理由为：

∵四边形的对角线互相平分，∴这个四边形是平行四边形，

∵四边形是“等邻边四边形”，∴这个四边形有一组邻边相等，

∴这个“等邻边四边形”是菱形；

②∵∠ABC=90°，AB=2，BC=1，

∴AC= ，

∵将Rt△ABC平移得到△A′B′C′，

∴BB′=AA′，A′B′∥AB，A′B′=AB=2，B′C′=BC=1，A′C′=AC= ，

（I）如图1，当AA′=AB时，BB′=AA′=AB=2；

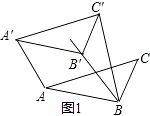
（II）如图2，当AA′=A′C′时，BB′=AA′=A′C′= ；

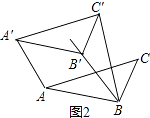
（III）当A′C′=BC′= 时，

如图3，延长C′B′交AB于点D，则C′B′⊥AB，

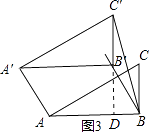
∵BB′平分∠ABC，

∴∠ABB′= ∠ABC=45°，

∴∠BB′D=′∠ABB′=45°

∴B′D=B，

设B′D=BD=x，

则C′D=x+1，BB′= x，

∵在Rt△BC′D中，BD2+（C′D）2=（BC′）2

∴x2+（x+1）2=（ ）2，

解得：x1=1，x2=﹣2（不合题意，舍去），

∴BB′= x=

（Ⅳ）当BC′=AB=2时，如图4，与（Ⅲ）方法一同理可得：BD2+（C′D）2=（BC′）2，

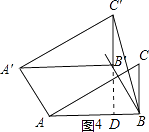
设B′D=BD=x，

则x2+（x+1）2=22，

解得： x1= ，x2= （不合题意，舍去），

∴BB′= x=

（3）

解：BC，CD，BD的数量关系为：BC2+CD2=2BD2，如图5，

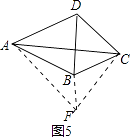
∵AB=AD，

∴将△ADC绕点A旋转到△ABF，连接CF，

∴△ABF≌△ADC，

∴∠ABF=∠ADC，∠BAF=∠DAC，AF=AC，FB=CD，

∴∠BAD=∠CAF， =1，

∴△ACF∽△ABD，

∴ = ，∴ BD，

∵∠BAD+∠ADC+∠BCD+∠ABC=360°，

∴∠ABC+∠ADC﹣360°﹣（∠BAD+∠BCD）=360°﹣90°=270°，

∴∠ABC+∠ABF=270°，

∴∠CBF=90°，

∴BC2+FB2=CF2=（ BD）2=2BD2，

∴BC2+CD2=2BD2．

【解析】（1）由“等邻边四边形”的定义易得出结论；（2）①先利用平行四边形的判定定理得平行四边形，再利用“等邻边四边形”定义得邻边相等，得出结论；②由平移的性质易得BB′=AA′，A′B′∥AB，A′B′=AB=2，B′C′=BC=1，A′C′=AC= ，再利用“等邻边四边形”定义分类讨论，由勾股定理得出结论；（3）由旋转的性质可得△ABF≌△ADC，由全等性质得∠ABF=∠ADC，∠BAF=∠DAC，AF=AC，FB=CD，利用相似三角形判定得△ACF∽△ABD，由相似的性质和四边形内角和得∠CBF=90°，利用勾股定理，等量代换得出结论．
【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案，需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．