

分析 (1)通过解直角三角形即可得到结果;
(2)过点B作BD⊥AO交AO的延长线于D,通过解直角三角形求得BD的长,由C、O′、B′三点共线可得结果,计算O′B′+O′C-BD即可求解.
解答 解:(1)∵O′C⊥OA于C,OA=OB=24cm,
∴sin∠CAO′=$\frac{O'C}{O'A}=\frac{O'C}{OA}=\frac{1}{2}$,
∴∠CAO′=30°.
(2)过点B作BD⊥AO交AO的延长线于D.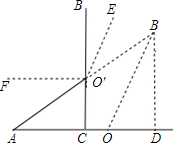
∵sin∠BOD=$\frac{BD}{OB}$,
∴BD=OB•sin∠BOD,
∵∠AOB=120°,
∴∠BOD=60°,
∴BD=OB•sin∠BOD=24×$\frac{{\sqrt{3}}}{2}=12\sqrt{3}$.
∵O′C⊥OA,∠CAO′=30°,
∴∠AO′C=60°.
∵∠AO′B′=120°,
∴∠AO′B′+∠AO′C=180°.
∴O′B′+O′C-BD=24+12-$12\sqrt{3}$=36-$12\sqrt{3}$.
∴显示屏的顶部B′比原来升高了(36-$12\sqrt{3}$)cm.
点评 本题考查了解直角三角形的应用,旋转的性质,正确的画出图形是解题的关键.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 初二 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 初三 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com