
°æƒø°ø»ÁÕº1£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨≈◊ŒÔœþæ≠π˝◊¯±Í‘≠µ„O£¨µ„A£®6£¨©Å6 ![]() £©£¨«““‘y÷·Œ™∂‘≥∆÷·£Æ
£©£¨«““‘y÷·Œ™∂‘≥∆÷·£Æ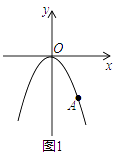
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©»ÁÕº2£¨π˝µ„B£®0£¨©Å ![]() £©◊˜x÷·µƒ∆Ω––œþl£¨µ„C‘⁄÷±œþl…œ£¨µ„D‘⁄y÷·◊Û≤ýµƒ≈◊ŒÔœþ…œ£¨¡¨Ω”DB£¨“‘µ„DŒ™‘≤–ƒ£¨“‘DBŒ™∞Îæ∂ª≠‘≤£¨°—D”Îx÷·œýΩª”⁄µ„M£¨N£®µ„M‘⁄µ„Nµƒ◊Û≤ý£©£¨¡¨Ω”CN£¨µ±MN=CN ±£¨«Û»ÒΩ«°œMNCµƒ∂» ˝£ª
£©◊˜x÷·µƒ∆Ω––œþl£¨µ„C‘⁄÷±œþl…œ£¨µ„D‘⁄y÷·◊Û≤ýµƒ≈◊ŒÔœþ…œ£¨¡¨Ω”DB£¨“‘µ„DŒ™‘≤–ƒ£¨“‘DBŒ™∞Îæ∂ª≠‘≤£¨°—D”Îx÷·œýΩª”⁄µ„M£¨N£®µ„M‘⁄µ„Nµƒ◊Û≤ý£©£¨¡¨Ω”CN£¨µ±MN=CN ±£¨«Û»ÒΩ«°œMNCµƒ∂» ˝£ª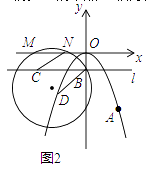
£®3£©»ÁÕº3£¨‘⁄£®2£©µƒÃıº˛œ¬£¨∆Ω“∆÷±œþCNæ≠π˝µ„A£¨”Î≈◊ŒÔœþœýΩª”⁄¡Ì“ªµ„E£¨π˝µ„A◊˜x÷·µƒ∆Ω––œþm£¨π˝µ„£®©Å3£¨0£©◊˜y÷·µƒ∆Ω––œþn£¨÷±œþm”Î÷±œþnœýΩª”⁄µ„S£¨µ„R‘⁄÷±œþn…œ£¨µ„P‘⁄EAµƒ—”≥§œþ…œ£¨¡¨Ω”SP£¨“‘SPŒ™±þœÚ…œ◊˜µ»±þ°˜SPQ£¨¡¨Ω”RQ£¨PR£¨»Ù°œQRS=60°„£¨œþ∂ŒPRµƒ÷–µ„K«°∫√¬‰‘⁄≈◊ŒÔœþ…œ£¨«ÛQµ„◊¯±Í£Æ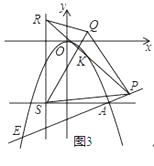
°æ¥∞∏°ø
£®1£©
Ω‚£∫…Ëπ˝◊¯±Í‘≠µ„O£¨µ„A£®6£¨©Å6 ![]() £©£¨«““‘y÷·Œ™∂‘≥∆÷·µƒ≈◊ŒÔœþŒ™y=ax2£¨
£©£¨«““‘y÷·Œ™∂‘≥∆÷·µƒ≈◊ŒÔœþŒ™y=ax2£¨
‘Ú©Å6 ![]() =36a£¨
=36a£¨
°ýa=©Å ![]() £¨
£¨
°ýy=©Å ![]() x2
x2
£®2£©
Ω‚£∫»ÁÕº2÷–£¨◊˜CF°ÕMN”⁄F£¨…Ë°—D”Îx÷·µƒΩªµ„Œ™£®x£¨0£©£¨D£®m£¨©Å ![]() m2£©£Æ
m2£©£Æ
‘Ú”–£®x©Åm£©2+£® ![]() m2£©2=m2+£®©Å
m2£©2=m2+£®©Å ![]() m2+
m2+ ![]() £©2£¨
£©2£¨
’˚¿Ìµ√x2©Å2mx+m2©Å3=0£¨
°ýx=m+ ![]() ªÚm©Å
ªÚm©Å ![]() £¨
£¨
°ýN£®m+ ![]() £¨0£©£¨M£®m©Å
£¨0£©£¨M£®m©Å ![]() £¨0£©
£¨0£©
°ýMN=2 ![]() £¨
£¨
‘⁄Rt°˜CFN÷–£¨°þ°œCFN=90°„£¨CN=MN=2 ![]() £¨CF=
£¨CF= ![]() £¨
£¨
°ýCN=2CF£¨
°ý°œCNF=30°„
£®3£©
Ω‚£∫»ÁÕº3÷–£¨

”…“‚ø…÷™∆Ω“∆÷±œþCNæ≠π˝µ„Aµƒ÷±œþµƒΩ‚Œˆ ΩŒ™y= ![]() x©Å8
x©Å8 ![]() £¨
£¨
º«÷±œþy= ![]() x©Å8
x©Å8 ![]() ”Î÷±œþx=©Å3µƒΩªµ„Œ™G£¨‘ÚG£®©Å3£¨©Å9
”Î÷±œþx=©Å3µƒΩªµ„Œ™G£¨‘ÚG£®©Å3£¨©Å9 ![]() £©£¨
£©£¨
°þm°Œx÷·£¨«“π˝µ„A£®6£¨©Å6 ![]() £©£¨
£©£¨
°ýS£®©Å3£¨©Å6 ![]() £©£¨
£©£¨
°ýSG=3 ![]() £¨AS=9£¨
£¨AS=9£¨
°ýtan°œ2= ![]() =
= ![]() £¨
£¨
°ý°œ2=60°„£¨
°ý°œ1=30°„£¨
°þ°œQRS=60°„
°ý°œQRS=°œ2£¨
°þ°œRSQ+°œQSP=°œ2+°œSPG£¨°œQSP=°œ2=60°„£¨
°ý°œ3=°œ4£¨
‘⁄°˜SQR∫Õ°˜PSG÷–£¨
 £¨
£¨
°ý°˜SQR°’°˜PSH
°ýSR=PG£¨RQ=SG£¨
°ýRQ=SG=3 ![]() £¨◊˜DQ°Õn”⁄D£¨
£¨◊˜DQ°Õn”⁄D£¨
°ýQRD=60°„£¨
°ýDQ= ![]() DR=
DR= ![]() RQ=
RQ= ![]() £¨
£¨
°ýRD= ![]() QR=
QR= ![]() £¨
£¨
°þn «π˝£®©Å3£¨0£©”Îy÷·∆Ω––µƒ÷±œþ£¨…ËR£®©Å3£¨b£©£¨º«n”Îx÷·µƒΩªµ„Œ™M£¨‘ÚRM=b£¨
°þS£®©Å3£¨©Å6 ![]() £©£¨
£©£¨
°ýMS=6 ![]() £¨
£¨
°ýSR=RM+MS=b+6 ![]() =PG£¨◊˜PH°Õn”⁄H£¨
=PG£¨◊˜PH°Õn”⁄H£¨
°þ°œ2=60°„£¨
°ýGH= ![]() PG=
PG= ![]() £®b+6
£®b+6 ![]() £©£¨
£©£¨
°ýMH=MG©ÅHG=9 ![]() ©Å
©Å ![]() £®b+6
£®b+6 ![]() £©=6
£©=6 ![]() ©Å
©Å ![]() b£¨
b£¨
°ýP£®6+ ![]() b£¨
b£¨ ![]() b©Å6
b©Å6 ![]() £©£¨
£©£¨
°þK «PR÷–µ„£¨
°ýK£® ![]() +
+ ![]() b£¨
b£¨ ![]() b©Å3
b©Å3 ![]() £©£¨
£©£¨
Œ™¡À∑Ω±„£¨º«K£®x£¨y£©£¨º¥x= ![]() +
+ ![]() b£¨y=
b£¨y= ![]() b©Å3
b©Å3 ![]() £¨œ˚»•bµ√y=
£¨œ˚»•bµ√y= ![]() x©Å
x©Å ![]()
![]() £¨
£¨
°ý÷–µ„K‘⁄÷±œþy= ![]() ©Å
©Å ![]() …œ‘À∂Ø£¨
…œ‘À∂Ø£¨
”… 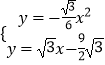 œ˚»•yµ√µΩx2+6x©Å27=0£¨
œ˚»•yµ√µΩx2+6x©Å27=0£¨
°ýx=3ªÚ©Å9£®…·∆˙£©£¨
°ýx=3£¨¥˙»Îx= ![]() +
+ ![]() bµ√µΩb=2
bµ√µΩb=2 ![]() £¨
£¨
°ýRM=2 ![]() £¨DM=RM©ÅRD=2
£¨DM=RM©ÅRD=2 ![]() ©Å
©Å ![]()
![]() =
= ![]()
![]() £¨
£¨
°þ ![]() ©Å3=
©Å3= ![]() £¨
£¨
°ýµ„Qµƒ◊¯±ÍŒ™£® ![]() £¨
£¨ ![]()
![]() £©
£©
°æΩ‚Œˆ°ø£®1£©…Ëπ˝◊¯±Í‘≠µ„O£¨µ„A£®6£¨©Å6 ![]() £©£¨«““‘y÷·Œ™∂‘≥∆÷·µƒ≈◊ŒÔœþŒ™y=ax2 £¨ µ„A¥˙»Î«Û≥ˆaº¥ø…£Æ£®2£©»ÁÕº2÷–£¨◊˜CF°ÕMN”⁄F£¨…Ë°—D”Îx÷·µƒΩªµ„Œ™£®x£¨0£©£¨D£®m£¨©Å
£©£¨«““‘y÷·Œ™∂‘≥∆÷·µƒ≈◊ŒÔœþŒ™y=ax2 £¨ µ„A¥˙»Î«Û≥ˆaº¥ø…£Æ£®2£©»ÁÕº2÷–£¨◊˜CF°ÕMN”⁄F£¨…Ë°—D”Îx÷·µƒΩªµ„Œ™£®x£¨0£©£¨D£®m£¨©Å ![]() m2£©£¨∏˘æð∞Îæ∂œýµ»¡–≥ˆ∑Ω≥㨫Û≥ˆM°¢N◊¯±Í£¨Õ∆≥ˆMN=2
m2£©£¨∏˘æð∞Îæ∂œýµ»¡–≥ˆ∑Ω≥㨫Û≥ˆM°¢N◊¯±Í£¨Õ∆≥ˆMN=2 ![]() £¨‘⁄Rt°˜CFN÷–£¨”…CN=2CFÕ∆≥ˆ°œFNC=30°„º¥ø…Ω‚æˆŒ £ƣ®3£©»ÁÕº3÷–£¨”…“‚ø…÷™∆Ω“∆÷±œþCNæ≠π˝µ„Aµƒ÷±œþµƒΩ‚Œˆ ΩŒ™y=
£¨‘⁄Rt°˜CFN÷–£¨”…CN=2CFÕ∆≥ˆ°œFNC=30°„º¥ø…Ω‚æˆŒ £ƣ®3£©»ÁÕº3÷–£¨”…“‚ø…÷™∆Ω“∆÷±œþCNæ≠π˝µ„Aµƒ÷±œþµƒΩ‚Œˆ ΩŒ™y= ![]() x©Å8
x©Å8 ![]() £¨º«÷±œþy=
£¨º«÷±œþy= ![]() x©Å8
x©Å8 ![]() ”Î÷±œþx=©Å3µƒΩªµ„Œ™G£¨‘ÚG£®©Å3£¨©Å9
”Î÷±œþx=©Å3µƒΩªµ„Œ™G£¨‘ÚG£®©Å3£¨©Å9 ![]() £©£¨”…°˜SQR°’°˜PSH£¨Õ∆≥ˆSR=PG£¨RQ=SG£¨Õ∆≥ˆRQ=SG=3
£©£¨”…°˜SQR°’°˜PSH£¨Õ∆≥ˆSR=PG£¨RQ=SG£¨Õ∆≥ˆRQ=SG=3 ![]() £¨◊˜DQ°Õn”⁄D£¨º«n”Îx÷·µƒΩªµ„Œ™M£¨‘ÚRM=b£¨”…S£®©Å3£¨©Å6
£¨◊˜DQ°Õn”⁄D£¨º«n”Îx÷·µƒΩªµ„Œ™M£¨‘ÚRM=b£¨”…S£®©Å3£¨©Å6 ![]() £©£¨Õ∆≥ˆMS=6
£©£¨Õ∆≥ˆMS=6 ![]() £¨ø…µ√P£®6+
£¨ø…µ√P£®6+ ![]() b£¨
b£¨ ![]() b©Å6
b©Å6 ![]() £©£¨‘Ÿ«Û≥ˆPR÷–µ„k◊¯±Í£¨÷§√˜k‘⁄÷±œþy=
£©£¨‘Ÿ«Û≥ˆPR÷–µ„k◊¯±Í£¨÷§√˜k‘⁄÷±œþy= ![]() ©Å
©Å ![]() …œ‘À∂Ø£¨”…
…œ‘À∂Ø£¨”… 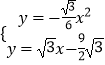 œ˚»•yµ√µΩx2+6x©Å27=0£¨x=3ªÚ©Å9£®…·∆˙£©£¨x=3£¨¥˙»Îx=
œ˚»•yµ√µΩx2+6x©Å27=0£¨x=3ªÚ©Å9£®…·∆˙£©£¨x=3£¨¥˙»Îx= ![]() +
+ ![]() bµ√µΩb=2
bµ√µΩb=2 ![]() £¨”…¥Àº¥ø…Ω‚æˆŒ £Æ
£¨”…¥Àº¥ø…Ω‚æˆŒ £Æ
°æøºµ„æ´Œˆ°øπÿ”⁄±æÂøº≤ȵƒ∂˛¥Œ∫Ø ˝µƒÕºœÛ∫Õ∂˛¥Œ∫Ø ˝µƒ–‘÷ £¨–Ë“™¡ÀΩ‚∂˛¥Œ∫Ø ˝ÕºœÒπÿº¸µ„£∫1°¢ø™ø⁄∑ΩœÚ2°¢∂‘≥∆÷· 3°¢∂•µ„ 4°¢”Îx÷·Ωªµ„ 5°¢”Îy÷·Ωªµ„£ª‘ˆºı–‘£∫µ±a>0 ±£¨∂‘≥∆÷·◊Û±þ£¨yÀÊx‘ˆ¥Û∂¯ºı–°£ª∂‘≥∆÷·”“±þ£¨yÀÊx‘ˆ¥Û∂¯‘ˆ¥Û£ªµ±a<0 ±£¨∂‘≥∆÷·◊Û±þ£¨yÀÊx‘ˆ¥Û∂¯‘ˆ¥Û£ª∂‘≥∆÷·”“±þ£¨yÀÊx‘ˆ¥Û∂¯ºı–°≤≈ƒÐµ√≥ˆ’˝»∑¥∞∏£Æ


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨æÿ–ŒABCD÷–£¨AB=16cm£¨AD=6cm£¨∂ص„P°¢Q∑÷±¥”A°¢C¡Ωµ„Õ¨ ±≥ˆ∑¢£¨µ„P“‘3cm/sµƒÀŸ∂»œÚµ„B“∆∂Ø£¨“ª÷±µΩ¥Ôµ„BŒ™÷𣨵„Q“‘2cm/sµƒÀŸ∂»œÚµ„D“∆∂Ø£Æ
£®1£©P°¢Q¡Ωµ„¥”≥ˆ∑¢ø™ º£¨æ≠π˝º∏√Î ±£¨Àƒ±þ–ŒPBCQµƒ√ʪ˝Œ™33cm2£ø
£®2£©P°¢Q¡Ωµ„¥”≥ˆ∑¢ø™ º£¨æ≠π˝º∏√Î ±£¨µ„P∫Õµ„Qµƒæý¿ÎŒ™10cm£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡ÀΩ‚±æ–£æ≈ƒÍº∂—ß…˙∆⁄ƒ© ˝—ßøº ‘«Èøˆ£¨–°¡¡‘⁄æ≈ƒÍº∂Àʪ˙≥È»°¡À“ª≤ø∑÷—ß…˙µƒ∆⁄ƒ© ˝—ß≥…º®Œ™—˘±æ£¨∑÷Œ™A£®100©Å90∑÷£©°¢B£®89°´80∑÷£©°¢C£®79°´60∑÷£©°¢D£®59°´0∑÷£©Àƒ∏ˆµ»º∂Ω¯––Õ≥º∆£¨≤¢Ω´Õ≥º∆Ω·π˚ªÊ÷∆≥…»Áœ¬Õ≥º∆Õº£¨«Îƒ„∏˘æðÕ≥º∆ÕºΩ‚¥“‘œ¬Œ £∫
£®1£©’‚¥ŒÀʪ˙≥È»°µƒ—ß…˙π≤”–∂ý…Ÿ»À£ø
£®2£©«Î≤π»´Ãı–ŒÕ≥º∆Õº£ª
£®3£©’‚∏ˆ—ß–£æ≈ƒÍº∂π≤”–—ß…˙1200»À£¨»Ù∑÷ ˝Œ™80∑÷£®∫¨80∑÷£©“‘…œŒ™”≈–„£¨«Îπ¿º∆’‚¥Œæ≈ƒÍº∂—ß…˙∆⁄ƒ© ˝—ßøº ‘≥…º®Œ™”≈–„µƒ—ß…˙»À ˝¥Û‘º”–∂ý…Ÿ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™E «’˝∑Ω–ŒABCDµƒ±þCDµƒ÷–µ„£¨µ„F‘⁄BC…œ£¨«“°œDAE=°œFAE£¨
«Û÷§£∫AF=AD+CF£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øº◊°¢““¡Ω»À¿˚”√≤ªÕ¨µƒΩªÕ®π§æþ£¨—ÿÕ¨“ª¬∑œþ¥”Aµÿ≥ˆ∑¢«∞Õ˘Bµÿ£¨º◊≥ˆ∑¢1h∫Û£¨““≥ˆ∑¢£Æ…˺◊”ÎAµÿœýæýyº◊£®km£©£¨““”ÎAµÿœýæýy““£®km£©£¨º◊¿Îø™Aµÿ ±º‰Œ™x£®h£©£¨yº◊°¢y““”Îx÷ƺ‰µƒ∫Ø ˝ÕºœÛ»ÁÕºÀ˘ æ£Æ
£®1£©º◊µƒÀŸ∂» «°° °°km/h£Æ
£®2£©«Î∑÷±«Û≥ˆyº◊°¢y““”Îx÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£Æ
£®3£©µ±““”ÎAµÿœýæý240km ±£¨º◊”ÎBµÿœýæý∂ý…Ÿ«ß√◊£ø

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£∫‘⁄Àƒ±þ–ŒABCD÷–£¨AB£ΩAD£¨°œBAD£Ω120°„£¨°œB£Ω°œADC£Ω90°„£ÆE°¢F∑÷± «BC°¢CD…œµƒµ„£Æ«“°œEAF£Ω60°„£ÆÃΩæøÕº÷–œþ∂ŒBE°¢EF°¢FD÷ƺ‰µƒ ˝¡øπÿœµ£Æ
–°ÕıÕ¨—ßÃΩæø¥ÀŒ µƒ∑Ω∑® «£¨—”≥§FDµΩµ„G£¨ πDG£ΩBE£Æ¡¨Ω·AG£¨œ»÷§√˜°˜ABE°’°˜ADG£¨‘Ÿ÷§√˜°˜AEF°’°˜AGF£¨ø…µ√≥ˆΩ·¬€£¨À˚µƒΩ·¬€”¶ «°° °°£ª

ÃΩÀ˜—”…Ï£∫
»ÁÕº2£¨»Ù‘⁄Àƒ±þ–ŒABCD÷–£¨AB£ΩAD£¨°œB£´°œD£Ω180°„£ÆE°¢F∑÷± «BC°¢CD…œµƒµ„£¨«“°œEAF£Ω![]() °œBAD£¨…œ ˆΩ·¬€ «∑Ò»‘»ª≥…¡¢£¨≤¢Àµ√˜¿Ì”…£ª
°œBAD£¨…œ ˆΩ·¬€ «∑Ò»‘»ª≥…¡¢£¨≤¢Àµ√˜¿Ì”…£ª
µº ”¶”√£∫
»ÁÕº3£¨‘⁄ƒ≥¥Œæ¸ ¬—ðœ∞÷–£¨Ω¢Õߺ◊‘⁄÷∏ª”÷––ƒ£®O¥¶£©±±∆´Œ˜30°„µƒA¥¶£¨Ω¢Õß““‘⁄÷∏ª”÷––ƒƒœ∆´∂´70°„µƒB¥¶£¨≤¢«“¡ΩΩ¢ÕßµΩ÷∏ª”÷––ƒµƒæý¿Îœýµ»£¨Ω”µΩ––∂Ø÷∏¡Ó∫Û£¨Ω¢Õߺ◊œÚ’˝∂´∑ΩœÚ“‘60∫£¿Ô/–° ±µƒÀŸ∂»«∞Ω¯£¨Ω¢Õß““—ÿ±±∆´∂´50°„µƒ∑ΩœÚ“‘80∫£¿Ô/–° ±µƒÀŸ∂»«∞Ω¯1.5–° ±∫Û£¨÷∏ª”÷––ƒπ€≤‚µΩº◊°¢““¡ΩΩ¢Õß∑÷±µΩ¥ÔE£¨F¥¶£¨«“¡ΩΩ¢Õß÷ƺ‰µƒº–Ω«Œ™70°„£¨ ‘«Û¥À ±¡ΩΩ¢Õß÷ƺ‰µƒæý¿Î£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨°˜ABC÷–£¨AB=AC£¨AD°ÕBC£¨CE°ÕAB£¨AE=CE£Æ«Û÷§£∫ 
£®1£©°˜AEF°’°˜CEB£ª
£®2£©AF=2CD£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®1£©»ÁÕº1£¨‘⁄Àƒ±þ–ŒABCD÷–£¨AB=CB£¨AD=CD£Æ«Û÷§£∫°œC=°œA£Æ
£®2£©»ÁÕº2£¨µ„B°¢F°¢C°¢E‘⁄“ªÃı÷±œþ…œ£¨FB=CE£¨AB°ŒED£¨AC°ŒFD£Æ«Û÷§£∫AB=DE£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨µ„A°¢B°¢C∑÷±Œ™◊¯±Í÷·…œ…œµƒ»˝∏ˆµ„£¨«“OA=1£¨OB=3£¨OC=4£¨
£®1£©«Ûæ≠π˝A°¢B°¢C»˝µ„µƒ≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷– «∑ҥʑ⁄“ªµ„P£¨ πµ√“‘“‘µ„A°¢B°¢C°¢PŒ™∂•µ„µƒÀƒ±þ–ŒŒ™¡‚–Œ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆµ„Pµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£ª
£®3£©»Ùµ„MŒ™∏√≈◊ŒÔœþ…œ“ª∂ص„£¨‘⁄£®2£©µƒÃıº˛œ¬£¨«Î«Û≥ˆµ±|PM©ÅAM|µƒ◊Ó¥Û÷µ ±µ„Mµƒ◊¯±Í£¨≤¢÷±Ω”–¥≥ˆ|PM©ÅAM|µƒ◊Ó¥Û÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com