
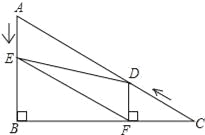
【题目】如图,在Rt△ABC中,∠B=90°,BC=![]() ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.

【答案】见解析
【解析】试题分析: (1)在△DFC中,∠DFC=90°,∠C=30°,由已知条件求证;
(2)求得四边形AEFD为平行四边形,若使AEFD为菱形则需要满足的条件及求得;
(3)①∠EDF=90°时,四边形EBFD为矩形.在直角三角形AED中求得AD=2AE即求得.
②∠DEF=90°时,由(2)知EF∥AD,则得∠ADE=∠DEF=90°,求得AD=AEcos60°列式得.
③∠EFD=90°时,此种情况不存在.
(1)证明:在△DFC中,∠DFC=90°,∠C=30°,DC=2t,
∴DF=t.
又∵AE=t,
∴AE=DF.
(2)解:能.理由如下:
∵AB⊥BC,DF⊥BC,
∴AE∥DF.
又AE=DF,
∴四边形AEFD为平行四边形.
∵AB=BCtan30°=![]() =5,
=5,
∴AC=2AB=10.
∴AD=AC﹣DC=10﹣2t.
若使AEFD为菱形,则需AE=AD,
即t=10﹣2t,t=![]() .
.
即当t=![]() 时,四边形AEFD为菱形.
时,四边形AEFD为菱形.
(3)解:①∠EDF=90°时,四边形EBFD为矩形.
在Rt△AED中,∠ADE=∠C=30°,
∴AD=2AE.
即10﹣2t=2t,t=![]() .
.
②∠DEF=90°时,由(2)四边形AEFD为平行四边形知EF∥AD,
∴∠ADE=∠DEF=90°.
∵∠A=90°﹣∠C=60°,
∴AD=AEcos60°.
即10﹣2t=![]() t,t=4.
t,t=4.
③∠EFD=90°时,此种情况不存在.
综上所述,当t=![]() 秒或4秒时,△DEF为直角三角形.
秒或4秒时,△DEF为直角三角形.


科目:初中数学 来源: 题型:
【题目】三角形内有一点到三角形三顶点的距离相等,则这点一定是三角形的( )
A. 三条中线的交点 B. 三边垂直平分线的交点
C. 三条高的交点 D. 三条角平分线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=![]() ,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )

A. ![]() B. 3 C. 2 D. 2
B. 3 C. 2 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连结AE,BD,设AE交CD于点F.
(1)求证:△ACE≌△DCB;
(2)求证:△ADF∽△BAD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,点O是正方形![]() 的一个顶点.如果两个正方形的边长都等于2,那么正方形
的一个顶点.如果两个正方形的边长都等于2,那么正方形![]() 绕O点无论怎样转动,两个正方形重叠的部分的面积是_____________.
绕O点无论怎样转动,两个正方形重叠的部分的面积是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】3月12日,团支部书记小颖带领全体团员参加植树活动,有一任务是在长25米的公路段旁栽一排树苗,每棵树的间距为5米,可他们手中只有一圈长20米的皮尺,怎样栽才能保证树苗在一条直线上,请你帮忙出出主意.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距900 m,甲、乙两人同时从A地出发,以相同速度匀速步行,20 min后到达B地,甲随后马上沿原路按原速返回,回到A地后在原地等候乙回来;乙则在B地停留10 min后也沿原路以原速返回A地,则甲、乙两人之间的距离s(m)与步行时间t(min)之间的函数关系可以用图象表示为 ( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com