
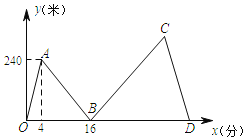
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人间的距离y(米)与甲出发的时间x(分)之间的关系如图中折线OA-AB-BC-CD所示.
(1)求线段AB的表达式,并写出自变量x的取值范围;
(2)求乙的步行速度;
(3)求乙比甲早几分钟到达终点?
【答案】(1)![]() ;(2)80米/分;(3)6分钟
;(2)80米/分;(3)6分钟
【解析】
(1)根据图示,设线段AB的表达式为:y=kx+b,把把(4,240),(16,0)代入得到关于k,b的二元一次方程组,解之,即可得到答案,
(2)根据线段OA,求出甲的速度,根据图示可知:乙在点B处追上甲,根据速度=路程÷时间,计算求值即可,
(3)根据图示,求出二者相遇时与出发点的距离,进而求出与终点的距离,结合(2)的结果,分别计算出相遇后,到达终点甲和乙所用的时间,二者的时间差即可所求答案.
(1)根据题意得:
设线段AB的表达式为:y=kx+b (4≤x≤16),
把(4,240),(16,0)代入得:
![]() ,
,
解得:![]() ,
,
即线段AB的表达式为:y= -20x+320 (4≤x≤16),
(2)又线段OA可知:甲的速度为:![]() =60(米/分),
=60(米/分),
乙的步行速度为:![]() =80(米/分),
=80(米/分),
答:乙的步行速度为80米/分,
(3)在B处甲乙相遇时,与出发点的距离为:240+(16-4)×60=960(米),
与终点的距离为:2400-960=1440(米),
相遇后,到达终点甲所用的时间为:![]() =24(分),
=24(分),
相遇后,到达终点乙所用的时间为:![]() =18(分),
=18(分),
24-18=6(分),
答:乙比甲早6分钟到达终点.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,数轴上 A、B 两点所对应的数分别是 a 和 b,且(a+5)2+|b﹣7|=0.
(1)求 a,b;A、B 两点之间的距离.
(2)有一动点 P 从点 A 出发第一次向左运动 1 个单位长度,然后在新的位置第二次运动,向右运动 2个单位长度,在此位置第三次运动,向左运动 3个单位长度…按照如此规律不断地左右运动,当运动到 2019次时,求点P所对应的数.
(3)在(2)的条件下,点 P在某次运动时恰好到达某一个位置,使点 P到点B的距离是点 P 到点 A 的距离的3倍?请直接写出此时点 P所对应的数,并分别写出是第几次运动.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发.苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:
(1)大巴与小车的平均速度各是多少?
(2)苏老师追上大巴的地点到基地的路程有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,…则第n个图形有__个小圆.

查看答案和解析>>
科目:初中数学 来源: 题型:
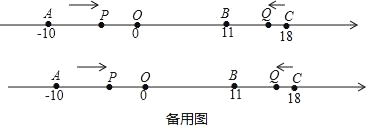
【题目】如图,在数轴上,点A表示﹣10,点B表示11,点C表示18.动点P从点A出发,沿数轴正方向以每秒2个单位的速度匀速运动;同时,动点Q从点C出发,沿数轴负方向以每秒1个单位的速度匀速运动.设运动时间为t秒.
(1)当t为何值时,P、Q两点相遇?相遇点M所对应的数是多少?
(2)在点Q出发后到达点B之前,求t为何值时,点P到点O的距离与点Q到点B的距离相等;
(3)在点P向右运动的过程中,N是AP的中点,在点P到达点C之前,求2CN﹣PC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年共有![]() 万名考生参加中考,为了了解这
万名考生参加中考,为了了解这![]() 万名考生的数学成绩,从中抽取了
万名考生的数学成绩,从中抽取了![]() 名考生的数学成绩进行统计分析,以下说法正确的有( )
名考生的数学成绩进行统计分析,以下说法正确的有( )
①这种调查采用了抽样调查的方式;②这种调查采用了全面调查的方式;③![]() 是样本容量;④每名考生的数学成绩是个体
是样本容量;④每名考生的数学成绩是个体
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌
粽子,每盒进价是40元,超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价![]() (元)之间的函数关系式;(4分)
(元)之间的函数关系式;(4分)
(2)当每盒售价定为多少元时,每天销售的利润![]() (元)最大?最大利润是多少?(6分)
(元)最大?最大利润是多少?(6分)
查看答案和解析>>
科目:初中数学 来源: 题型:
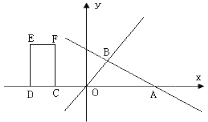
【题目】如图,直线![]() 交x轴于点A,交直线
交x轴于点A,交直线![]() 于点B(2,m).矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.(注:矩形就是长方形)
于点B(2,m).矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.(注:矩形就是长方形)
(1)求b、m的值;
(2)当矩形CDEF运动t秒时,请直接写出C、D两点的坐标(用含t的代数式表示)
(3)当点B在矩形CDEF的一边上时,求t的值;
(4)设CF、DE分别交折线OBA于M、N两点,当四边形MCDN为直角梯形时,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个运算流程.

例如:根据所给的运算流程可知,当 x=5 时,5×3﹣1=14<32,把 x=14 带入,14×3﹣1=41>32,则输出值为 41.
(1)填空:当 x=15 时,输出值为__________;当 x=6 时,输出值为__________-;
(2)若需要经过两次运算,才能运算出 y,求 x 的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com