
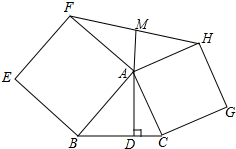
 如图,在△ABC的两边AB,AC上向△ABC外作正方形ABEF,ACGH,过点A作BC的垂线分别交BC于点D,交FH于点M,求证:FM=MH.
如图,在△ABC的两边AB,AC上向△ABC外作正方形ABEF,ACGH,过点A作BC的垂线分别交BC于点D,交FH于点M,求证:FM=MH. 分析 设∠FAM=α,∠HAM=β.根据三角形的面积公式得到S△FAM=$\frac{1}{2}$AF•AM•sinα,S△HAM=$\frac{1}{2}$AH•AM•sinβ,根据正方形的性质得到∠FAB=90°,于是得到∠FAM+∠BAD=90°,由已知条件得到∠ABD+∠BAD=90°,根据余角的性质得到∠ABD=∠FAM=α,同理∠ACD=∠AHM=β,根据正弦函数的定义得到AB•sinα=AD,AC•sinβ=AD,于是推出AF•sinα=AH•sinβ,于是得到S△FAM=S△HAM.即可得到结论.
解答 证明:设∠FAM=α,∠HAM=β.
∴S△FAM=$\frac{1}{2}$AF•AM•sinα,S△HAM=$\frac{1}{2}$AH•AM•sinβ,
∵四边形ABEF是正方形,
∴∠FAB=90°,
∴∠FAM+∠BAD=90°,
∵AD⊥BC,
∴∠ABD+∠BAD=90°,
∴∠ABD=∠FAM=α,同理∠ACD=∠AHM=β,
∵AB•sinα=AD,AC•sinβ=AD.
又∵AB=AF,AC=AH,
∴AF•sinα=AH•sinβ,
∴S△FAM=S△HAM.
∴FM=HM.
点评 本题考查了正方形的性质,三角形的面积公式,垂直的定义,三角函数,熟练掌握各性质定理是解题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
 如图,A、B两地有公路和铁路相连,在这条路上有一家食品厂,它到B地的距离是到A地的2倍,这家工厂从A地购买原料,制成食品卖到B地.已知公路运价为1.5元/(公里•吨),铁路运价为1元/(公里•吨),这两次运输(第一次:A地→食品厂,第二次:食品厂→B地)共支出公路运费15600元,铁路运费20600元.
如图,A、B两地有公路和铁路相连,在这条路上有一家食品厂,它到B地的距离是到A地的2倍,这家工厂从A地购买原料,制成食品卖到B地.已知公路运价为1.5元/(公里•吨),铁路运价为1元/(公里•吨),这两次运输(第一次:A地→食品厂,第二次:食品厂→B地)共支出公路运费15600元,铁路运费20600元.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
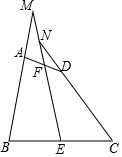 如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.
如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
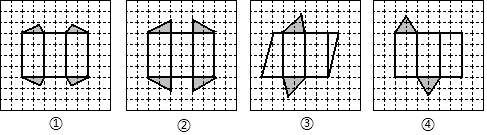
| A. | ①和④ | B. | ③和④ | C. | ①和② | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
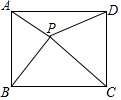 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PDA的面积分别为S1、S2、S3、S4,以下判断:
如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PDA的面积分别为S1、S2、S3、S4,以下判断:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com