
【题目】如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.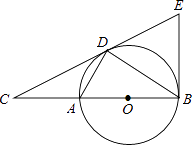
(1)判断直线CD和⊙O的位置关系,并说明理由.
(2)过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求∠BEC的正切值.
【答案】
(1)解:直线CD与⊙O的位置关系是相切.
理由:
连接OD,如图所示:
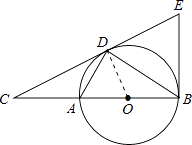
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠DBA=90°,
∵∠CDA=∠CBD,
∴∠DAB+∠CDA=90°,
∵OD=OA,
∴∠DAB=∠ADO,
∴∠CDA+∠ADO=90°,
即:OD⊥CE,
∴直线CD 是⊙O的切线.
即:直线CD 与⊙O的位置关系是相切.
(2)解:∵AC=2,⊙O的半径是3,
∴OC=2=3=5,OD=3,
在Rt△CDO中,由勾股定理得:CD=4.
∵CE切⊙O于D,EB切⊙O于B,
∴DE=EB,∠CBE=90°,
设DE=EB=x,
在Rt△CBE中,有勾股定理得:CE2=BE2+BC2,
则 (4+x)2=x2+(5+3)2,
解得:x=6,
即 BE=6,
∴tan∠BEC= ![]() ,
,
即:tan∠BEC= ![]() .
.
【解析】(1)连接OD,由直径所对的圆周角为直角得到∠ADB=90°,然后可得到∠CDA+∠ODA=90°,故此可得到直线和圆的位置关系;
(2)首先在Rt△CDO中依据勾股定理求得:CD的长,然后依据切线长定理得DE=EB,设DE=EB=x,在Rt△CBE中,由勾股定理得:CE2=BE2+BC2,可得到关于x的方程,从而可求得x的值,最后由正切函数的定义解得∠BEC的正切值即可.
【考点精析】本题主要考查了直线与圆的三种位置关系和切线的性质定理的相关知识点,需要掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,过半径为6的圆O上一点A作圆O的切线l,P为圆O的一个动点,作PH⊥l于点H,连接PA.如果PA=x,AH=y,那么下列图象中,能大致表示y与x的函数关系的是( )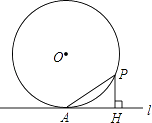
A.
B.
C.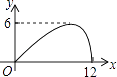
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校想了解学生参加课外体育锻炼情况,随机抽取本校40名学生进行问卷调查,统计整理并绘制了如下两幅尚不完整的统计图:
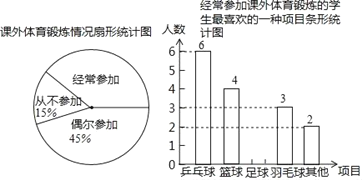
根据以上信息解答下列问题:
(1)课外体育锻炼情况统计图中,“经常参加”所对应的圆心角的度数为 ;
(2)补全条形统计图;
(3)该校共有800名学生,请估计全校学生中经常参加课外体育锻炼并喜欢的项目是 ,乒乓球的人数有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2mx+4m﹣8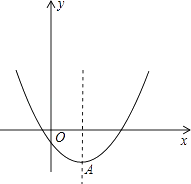
(1)当x≤2时,函数值y随x的增大而减小,求m的取值范围.
(2)以抛物线y=x2﹣2mx+4m﹣8的顶点A为一个顶点作该抛物线的内接正三角形AMN(M,N两点在拋物线上),请问:△AMN的面积是与m无关的定值吗?若是,请求出这个定值;若不是,请说明理由.
(3)若抛物线y=x2﹣2mx+4m﹣8与x轴交点的横坐标均为整数,求整数m的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边三角形△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边三角形△CBD,连接DA并延长,交y轴于点E.
(1)求证:△OBC≌△ABD
(2)在点C的运动过程中,∠CAD的度数是否会变化?如果不变,请求出∠CAD的度数;如果变化,请说明理由.
(3)当点C运动到什么位置时,以A,E,C为顶点的三角形是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了满足学生借阅图书的需求,计划购买一批新书.为此,该校图书管理员对一周内本校学生从图书馆借出各类图书的数量进行了统计,结果如下图.
请你根据统计图中的信息,解答下列问题:
(1)补全条形统计图和扇形统计图;
(2)该校学生最喜欢借阅哪类图书?
(3)该校计划购买新书共600本,若按扇形统计图中的百分比来相应地确定漫画、科普、文学、其它这四类图书的购买量,求应购买这四类图书各多少本?
(无原图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com